Zigurat Global Institute of Technology
Dimensionado columna interior en acero según criterio de esbeltez
Categorias

En el siguiente artículo vamos a estimar el pre-dimensionado de la sección de acero para una columna interior. Todo el contenido forma parte del Máster Internacional de Estructuras Metálicas y Mixtas de Zigurat. En este primer artículo nos centramos en la limitación de esbeltez para elementos comprimidos. La columna en estudio es de gran longitud (L=13.20m) y forma parte de un pórtico con dinteles en celosía de 38m de luz. 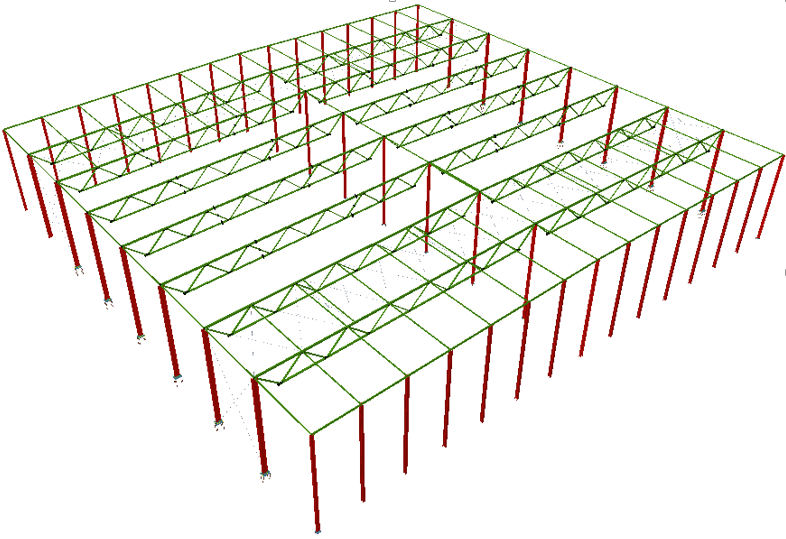 Figura 1 3D de la nave completa (3d nave.PNG)
Figura 1 3D de la nave completa (3d nave.PNG) 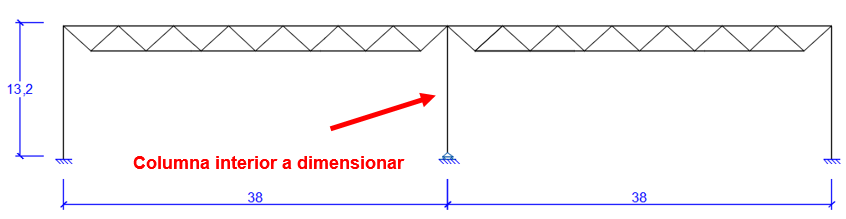 Figura 2 Geometría básica del pórtico tipo y columna interior (geometria.PNG)
Figura 2 Geometría básica del pórtico tipo y columna interior (geometria.PNG)
Estabilidad lateral del pórtico
Antes de abordar la resolución del caso tenemos que valorar cómo se va a comportar el pórtico frente a acciones laterales tales como el viento. Vamos a considerar que toda la estabilidad lateral del pórtico en su plano es aportada únicamente por los pilares extremos. Es decir. Imaginemos que el viento incide de izquierda a derecha. Será la columna exterior izquierda la que va a hacer frente a esta solicitación. Lo mismo ocurriría con la columna extrema exterior derecha si el viento soplase en sentido contrario. Los pilares exteriores se comportan en el plano del pórtico como empotrados a la cimentación y libres en cabeza, es decir, en ménsula. Ésta es la opción más desfavorable en el dimensionado de las columnas externas ya que derivamos toda la estabilidad del pórtico a la única rigidez de la columna sin considerar la colaboración de otros elementos estructurales como podría ser el propio dintel de cubierta o vigas contraviento. Respecto al plano de fachada, es decir, respecto al plano perpendicular al pórtico, los pilares exteriores se comportan como empotrados en la base y articulados en cabeza debido a la presencia de los tubos de compresión que atan todos los pilares de la nave en sus aleros. 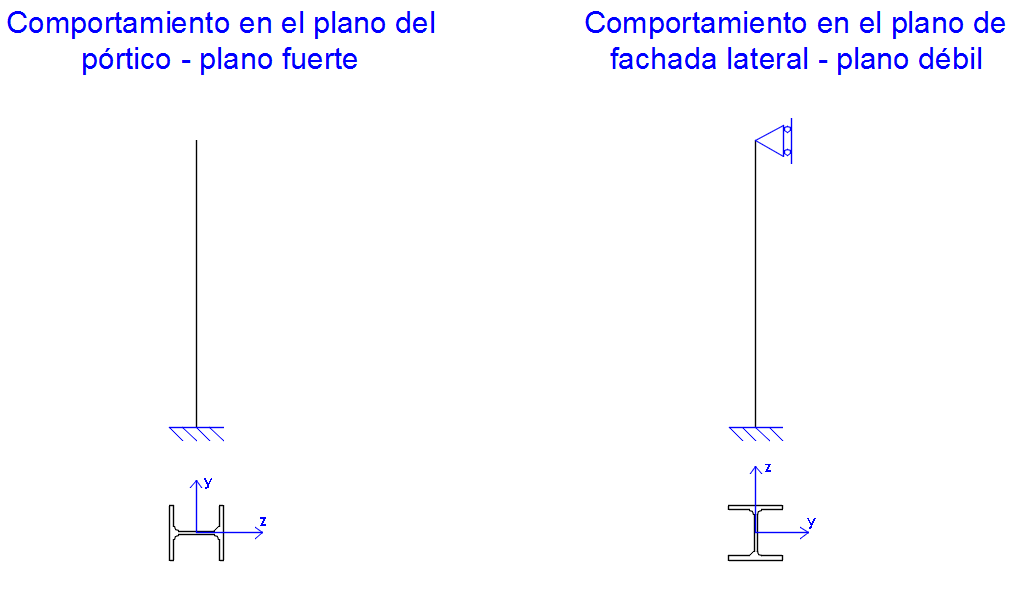 Figura 3 Condiciones de contorno de los pilares exteriores (pilar_exterior_estabilidad.PNG) Adicionalmente como consecuencia de estas cargas horizontales no se van a producir compresiones en el cordón superior de la celosía siendo ésta una de las principales ventajas de este sistema. Consecuentemente la columna interior, que es la que nos ocupa en este artículo, puede modelarse como articulada en la base ya que en términos de rigidez lateral no se considera su colaboración. En su dimensionado van a ser los esfuerzos axiles los que adquieran mayor protagonismo y, por lo tanto, para la columna interior podremos consideras las condiciones de estabilidad siguientes:
Figura 3 Condiciones de contorno de los pilares exteriores (pilar_exterior_estabilidad.PNG) Adicionalmente como consecuencia de estas cargas horizontales no se van a producir compresiones en el cordón superior de la celosía siendo ésta una de las principales ventajas de este sistema. Consecuentemente la columna interior, que es la que nos ocupa en este artículo, puede modelarse como articulada en la base ya que en términos de rigidez lateral no se considera su colaboración. En su dimensionado van a ser los esfuerzos axiles los que adquieran mayor protagonismo y, por lo tanto, para la columna interior podremos consideras las condiciones de estabilidad siguientes: 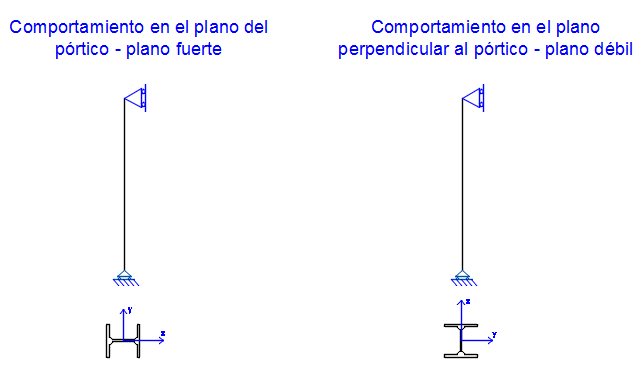 Figura 4 Condiciones de contorno del pilar interior (estabilidad_pilar_interior.PNG) Como consecuencia al criterio de estabilidad lateral que acabamos de establecer tenemos las longitudes de pandeo siguientes:
Figura 4 Condiciones de contorno del pilar interior (estabilidad_pilar_interior.PNG) Como consecuencia al criterio de estabilidad lateral que acabamos de establecer tenemos las longitudes de pandeo siguientes:  Arrancamos el proceso de dimensionado de la columna interior limitando su esbeltez reducida. Limitación de esbeltez reducida en piezas comprimidas A pesar de no ser una condición obligatoria, es recomendable que la esbeltez reducida o adimensional “λ ̅” en piezas comprimidas no sobrepase el valor de 2. La esbeltez adimensional o reducida “λ ̅” hace referencia a la raíz cuadrada entre la capacidad a axil de la sección “A·fy” y axil crítico de Euler “Ncr”. Esta esbeltez adimensional o reducida “λ ̅” también puede tomarse como la relación entre dos esbelteces: la esbeltez mecánica “λ” y la esbeltez límite de la teoría de Euler-Engesser “λ_R”. Esta esbeltez adimensional “λ ̅” es la que limitaremos a 2 para nuestra columna interior comprimida:
Arrancamos el proceso de dimensionado de la columna interior limitando su esbeltez reducida. Limitación de esbeltez reducida en piezas comprimidas A pesar de no ser una condición obligatoria, es recomendable que la esbeltez reducida o adimensional “λ ̅” en piezas comprimidas no sobrepase el valor de 2. La esbeltez adimensional o reducida “λ ̅” hace referencia a la raíz cuadrada entre la capacidad a axil de la sección “A·fy” y axil crítico de Euler “Ncr”. Esta esbeltez adimensional o reducida “λ ̅” también puede tomarse como la relación entre dos esbelteces: la esbeltez mecánica “λ” y la esbeltez límite de la teoría de Euler-Engesser “λ_R”. Esta esbeltez adimensional “λ ̅” es la que limitaremos a 2 para nuestra columna interior comprimida: 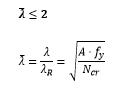 Donde: - λ : es la esbeltez mecánica que vale λ=L/i - λ_R : es le esbeltez límite de la teoría de Euler-Engesser y vale:
Donde: - λ : es la esbeltez mecánica que vale λ=L/i - λ_R : es le esbeltez límite de la teoría de Euler-Engesser y vale: 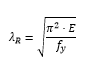 Despejando la esbeltez mecánica “λ” de la expresión anterior obtenemos una nueva expresión que relaciona la esbeltez mecánica únicamente con las características del material “E” y “fy“ del acero utilizado:
Despejando la esbeltez mecánica “λ” de la expresión anterior obtenemos una nueva expresión que relaciona la esbeltez mecánica únicamente con las características del material “E” y “fy“ del acero utilizado: 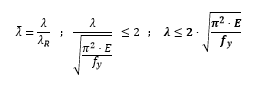 Por último sabemos que la esbeltez mecánica “λ” hallada es función de la longitud de pandeo "Lp" y del radio de giro de la sección "i":
Por último sabemos que la esbeltez mecánica “λ” hallada es función de la longitud de pandeo "Lp" y del radio de giro de la sección "i": 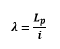 También deberemos valorar esta esbeltez mecánica “λ” en los dos planos de la sección, resultando:
También deberemos valorar esta esbeltez mecánica “λ” en los dos planos de la sección, resultando: 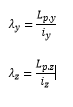 De estas expresiones conocemos la esbeltez mecánica “λ=2·√((π^2·E)/f_y ) ” así como las longitudes de pandeo “Lp.y e Lp.z”, por lo que podemos despejar los radios de giro mínimos necesarios “iy.mín e iz.mín” que nuestra sección de la columna deberá respetar: Estas expresiones resultan ser muy prácticas ya que nos permiten tantear una primera sección válida para la columna. Una vez repasado el procedimiento a seguir introducimos números a nuestro ejemplo y resumimos el PASO a PASO en una pequeña hoja de cálculo Mathcad que se podrá descargar próximamente.
De estas expresiones conocemos la esbeltez mecánica “λ=2·√((π^2·E)/f_y ) ” así como las longitudes de pandeo “Lp.y e Lp.z”, por lo que podemos despejar los radios de giro mínimos necesarios “iy.mín e iz.mín” que nuestra sección de la columna deberá respetar: Estas expresiones resultan ser muy prácticas ya que nos permiten tantear una primera sección válida para la columna. Una vez repasado el procedimiento a seguir introducimos números a nuestro ejemplo y resumimos el PASO a PASO en una pequeña hoja de cálculo Mathcad que se podrá descargar próximamente.
Creando la columna con Mathcad
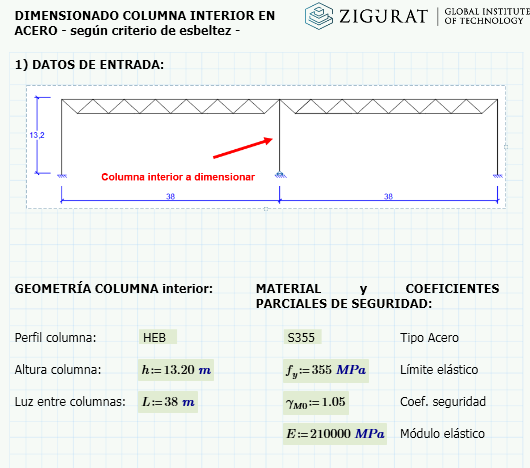 Geometría del pórtico y cargas de diseño de la columna interior
Geometría del pórtico y cargas de diseño de la columna interior  Condiciones de estabilidad
Condiciones de estabilidad  Predimensionado sección según limitación de esbeltez
Predimensionado sección según limitación de esbeltez  Planteamiento solución frente al problema de esbeltez En este primer artículo nos hemos centrado en la comprobación de esbeltez de la columna. Hemos dejado el análisis de la capacidad de la sección a compresión y el estudio de la resistencia a pandeo de la columna para un futuro artículo. Mientras tanto también se puede consultar el artículo “Placas de asiento: criterios de diseño y compresión simple” del BLOG de Zigurat, para el dimensionado de la placa base de una columna a compresión simple como la que acabamos de tratar.
Planteamiento solución frente al problema de esbeltez En este primer artículo nos hemos centrado en la comprobación de esbeltez de la columna. Hemos dejado el análisis de la capacidad de la sección a compresión y el estudio de la resistencia a pandeo de la columna para un futuro artículo. Mientras tanto también se puede consultar el artículo “Placas de asiento: criterios de diseño y compresión simple” del BLOG de Zigurat, para el dimensionado de la placa base de una columna a compresión simple como la que acabamos de tratar.
Este artículo está relacionado con el Máster Internacional en Estructuras Metálicas y Mixtas de Edificación.