Blog / Estructuras

Limitaciones de esbeltez para omitir el cálculo de flechas

Categorias

Introducción

El cálculo de flechas es un procedimiento farragoso, plagado además de datos de partida poco claros (flecha admisible en función de una rigidez de tabiquería no cuantificada, historia de cargas difícilmente previsible en proyecto, condiciones de temperatura y humedad desconocidos, etc.) que suman aún más incertidumbres a las intrínsecas al propio cálculo. Ante este panorama, la solución más efectiva para casos convencionales es limitar la esbeltez de los elementos, y así lo recogen ACI-318 y EHE-08.

Exención de cálculo de deflexiones en ACI-318

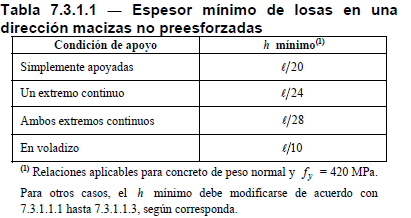El artículo 9.3.1.1 de ACI-318-14 dice “Para las vigas no preesforzadas que no soporten ni estén ligadas a particiones u otro tipo de elementos susceptibles de dañarse debido a deflexiones grandes, la altura total de la viga, h , no debe ser menor que los límites dados en la Tabla 9.3.1.1, a menos que se cumplan los límites de las deflexiones calculadas de 9.3.2.” Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Limita su aplicación a vigas que no soporten ni estén ligadas a particiones u otro tipo de elementos susceptibles de dañarse debido a la deformación de las vigas, lo que en cierto modo limita su uso. Tampoco podemos obviar la última frase, ya que admite esbelteces mayores, pero entonces exige calcular que la deflexión o flecha calculada es menor que la admisible. De la misma manera, el artículo 7.3.1.1 limita la esbeltez para losas unidireccionales “Para losas macizas no preesforzadas que no soporten o estén ligadas a particiones u otro tipo de construcción susceptibles de dañarse debido a deflexiones grandes, el espesor total de la losa h no debe ser menor que los límites de la Tabla 7.3.1.1, a menos que se cumpla con los límites para las deflexiones calculadas en 7.3.2.” Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Las esbelteces son algo mayores en el caso de losas, ya que solo soportan su peso y la carga que gravita sobre ellas, mientras que las vigas deben recibir la carga de las losas. Las tablas 8.3.1.1 y 8.3.1.2 recogen los espesores mínimos para losas bidireccionales para el caso de losas sin vigas interiores o con vigas interiores. Para no alargar en exceso este texto, dejamos su desarrollo para otra entrada.

Ejemplo

Tenemos un edificio con tabiquería flexible y estructura formada por marcos y losas unidireccionales. Los claros de vigas son de 6 m y los claros de losas son de 5 m. 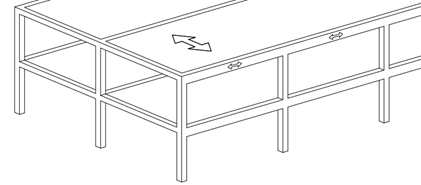Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Predimensionamos en primer lugar la losa. Según la tabla 7.3.1.1 la altura mínima para losas con un extremo continuo es L/24 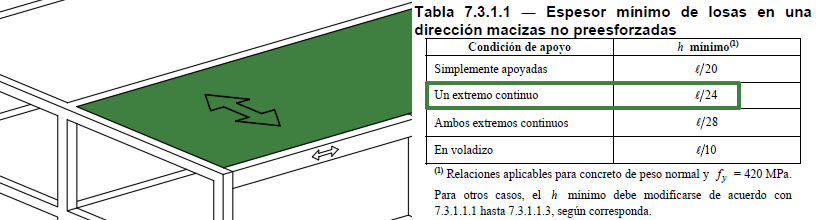Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Operamos y obtenemos una altura 20.83 cm, que podemos redondear a 21 cm. 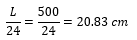Para las vigas tenemos dos situaciones: vigas con un extremo continuo (rojo) y vigas con ambos extremos continuos (azul). 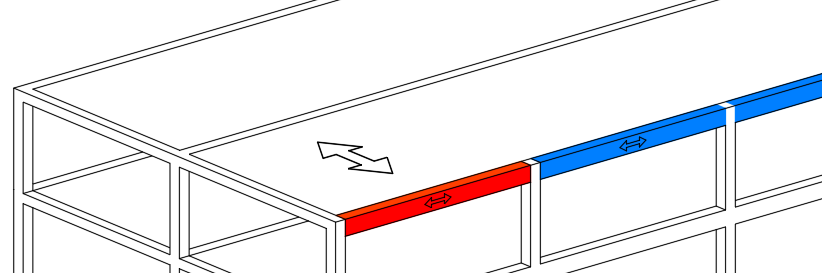Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Para las vigas con ambos extremos continuos, la altura mínima es 28.6 cm. 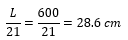Máster Internacional en Estructuras de Edificación con CYPE Para las vigas con un extremo continuo, la altura mínima es 32.4 cm, que podemos redondear a 35 cm. 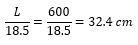Máster Internacional en Estructuras de Edificación con CYPE Esta diferencia refleja una de las cuestiones importantes en el trabajo con deformaciones:    La continuidad es fundamental para reducir deflexiones. Nos da además una pauta de diseño: Si reducimos el claro en los tramos extremos, optimizamos la altura de vigas.

Exención de cálculo de flechas en ACI-318

El artículo 50.2.2.1 de EHE-08 ofrece dos tablas con diversas relaciones entre la luz de la viga y su canto efectivo (l/h) que, si se cumplen, no es necesario calcular las flechas. La segunda tabla es para forjados, nos centraremos en la primera, que es genérica. 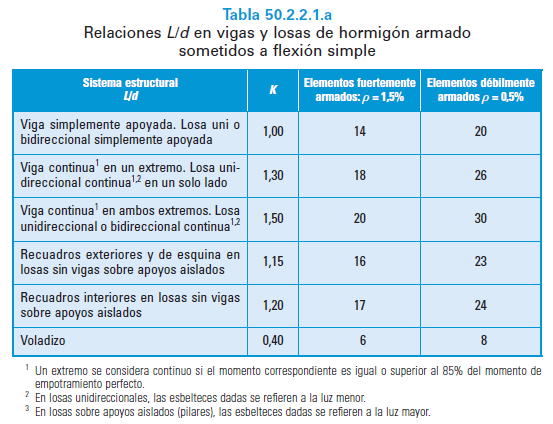Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas El siguiente esquema muestra los diferentes sistemas estructurales propuestos por la tabla: 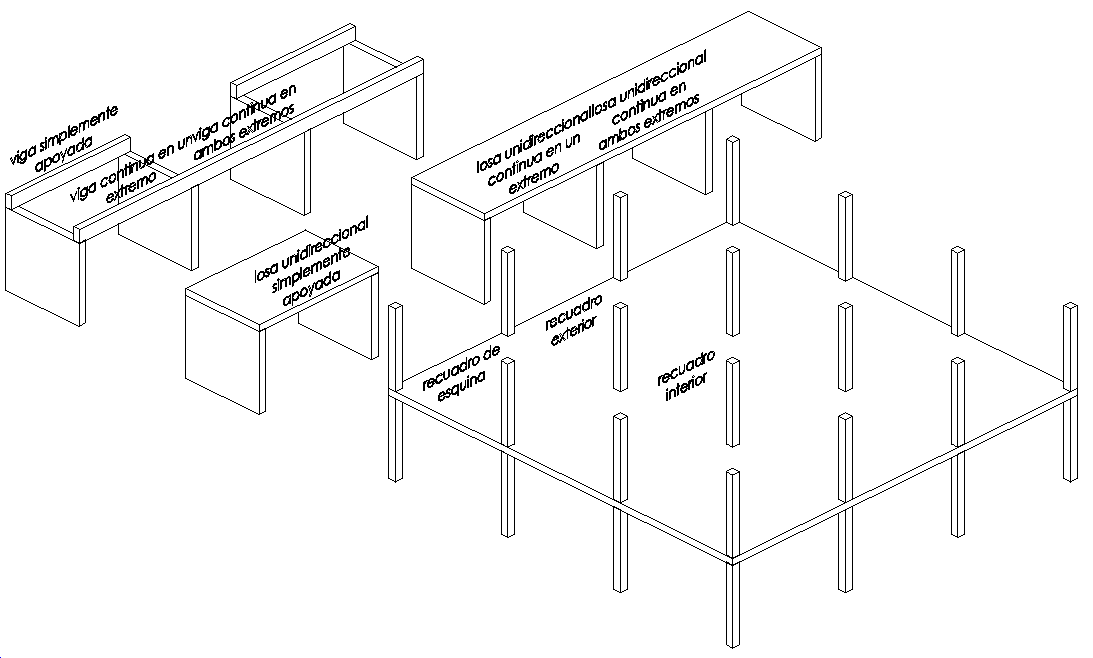Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Podemos observar que la esbeltez depende fuertemente de la continuidad. Por ejemplo, una viga continua en ambos extremos puede tener una esbeltez L/d=20, mientras que si es biapoyada no pasa de L/d=14. Por ejemplo, una viga continua de 5 m puede tener un canto útil 500/20=25 cm (pasaría a un canto total 30 cm), mientras que si es biapoyada debe tener al menos 500/14=35.7 cm (pasaría a un canto total de 40 cm). Las columnas correspondientes a elementos fuertemente armados y débilmente armados presuponen, respectivamente, una cuantía de armadura de tracción de 0,015 y 0,005. La columna K va más allá y permite hallar la relación L/d para diferentes valores de cuantías (cuantías necesarias para resistir las acciones, que indirectamente reflejan el efecto de las cargas) y tipos de hormigón. Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas El propio comentario indica que estos valores están calculados para hormigón con fck=30 N/mm² y acero trabajando, en servicio, a 310 N/mm². Este valor que correspondería a un acero B500S aplicando un coeficiente parcial de seguridad 1.15 al acero y un coeficiente promedio de 1.40 a las acciones, que es un valor habitual en edificios.

Ejemplo

Verificamos la necesidad de calcular la flecha en una viga 30×40 biapoyada de 5,25 m de luz bajo una carga permanente de 15 kN/m (incluido el peso propio de la viga) y una sobrecarga de 10 kN/m, suponiendo hormigón HA-30 y acero B 500 S (los que se mencionan en los comentarios de EHE-08 como referencia para la obtención de las tablas), con un recubrimiento mecánico de 50 mm. Suponemos que se ha calculado a flexión con el anejo 7 de EHE-08 aplicando los coeficientes parciales de seguridad 1,35 y 1,50 para las acciones permanentes y variables, respectivamente.

Solución

Aplicando la columna de elementos fuertemente armados obtenemos que L/d=14. Es decir, el canto útil debe ser al menos 5250/14=375 mm y por tanto el canto total debe ser al menos 375+50=425 mm. El canto de la viga propuesta es 40 cm = 400 mm, menor que el calculado para omitir la comprobación de flecha, en consecuencia hay que calcular la flecha. 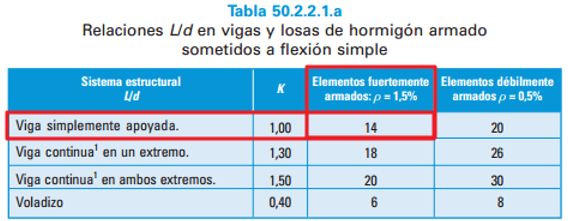Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Podemos apurar algo más aplicando la columna K. La carga de cálculo es 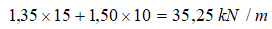Máster Internacional en Estructuras de Edificación con CYPE El momento flector máximo es 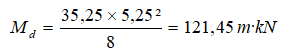Máster Internacional en Estructuras de Edificación con CYPE La armadura necesaria de tracción es Us1=382 kN, con fyd=500/1,15 supone 878 mm², que representa una cuantía 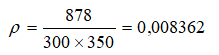Máster Internacional en Estructuras de Edificación con CYPE El valor K en la tabla 50.2.2.1.a de EHE-08 es 1,00. Aplicamos las fórmulas antes indicadas, con la ayuda de una hoja de cálculo y obtenemos una relación L/d=16,38, que supone un canto útil de 320 mm y con ello un canto total de 370 mm, inferior a 400 mm, por lo tanto no es preciso calcular flecha. 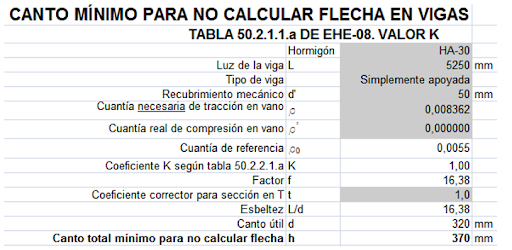Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Ciertamente el ejemplo es un tanto forzado, porque las cargas son sensiblemente bajas, pero precisamente por eso muestra claramente cómo el valor K permite tener en cuenta algo tan evidente como el estado de cargas.

Ejemplos del uso de K

Por último, para quien se vea con ganas de dar estrujar un poco más esta cuestión, veamos unos ejemplos de aplicación del coeficiente K. Asumimos HA-30 y B 500 S, coeficientes 1.35 y 1.50. Calculamos flectores mediante fórmulas simples para vigas biapoyadas o biempotradas y armados según el anejo 7 de EHE-08, con recubrimiento mecánico de 40 mm. Se considera, simplificadamente, que el peso propio de la viga está prorrateado en la hipótesis de peso propio. Agarraos fuerte que empezamos... E1 Como primer ejemplo, muy simple, supongamos una viga biapoyada de 5 m de luz. Vamos a la tabla 50.2.2.1ª de EHE-08 y tomamos L/d=14, ya que se trata de una viga y por lo tanto un elemento a priori fuertemente armado. El canto útil será no inferior a 35,7 cm. Concluimos, por lo tanto, una viga biapoyada de 5 m de luz y sección 25×40. E1a En primer lugar, forzaremos una situación que haga que la tabla de EHE-08 sea cierta. Supongamos que sobre la viga carga un forjado con un ancho de banda de 5,00 m, con un peso propio (incluyendo repercusión de peso propio de vigas, peso propio del forjado y peso propio de otros elementos constructivos) de 6,90 kN/m² y sobrecarga de 2,00 kN/m², es decir, un carga combinada de 12,32 kN/m², que en el ancho de banda de 5,00 m antes citado supone una carga total sobre la viga de 61,58 kN/m. Calculamos el flector positivo para la viga isostática y sale 192 m·kN. La armadura NECESARIA de tracción es de 1498 mm² (se cubre con 5ø20), lo que supone una cuantía de 0,015, que coincide con la cuantía que la tabla toma como referencia para elementos fuertemente armados. Aplicando las fórmulas de los comentarios de EHE-08 obtenemos que L/d=K·14; dado que K=1 (tabla 50.2.2.1.a), es obvio que L/d=14, tal como figura en la tabla. E1b Mantengamos la misma situación del ejemplo E1a pero supongamos que el peso propio (incluyendo repercusión de peso propio de vigas, peso propio del forjado y peso propio de otros elementos constructivos) es de 5,00 kN/m². El flector baja a 152 m·kN y el armado necesario se reduce a 1286 mm², lo que supone una cuantía de 0,0129. Aplicando la fórmula de los comentarios de EHE sale que L/d es menor o igual que 15, de modo que d es menor o igual que 33. Vemos que algo se redujo, aunque no lo suficiente para poder reducir la viga a 35 cm. E1c Supongamos ahora que reducimos el ancho de banda del forjado a 4 m. Si aplicaramos la tabla 50.2.2.1.a sin más, seguiríamos necesitando un canto de 40 cm. Ahora bien, repetimos el análisis y vemos que el momento flector positivo de cálculo baja a 122 m·kN, que supone un armado de 871 mm² y por lo tanto una cuantía de 0,0087. Aplicando la fórmula de los comentarios de EHE-08 obtenemos que L/d=16,17 y por lo tanto d=309 mm, lo que nos permitirá reducir la viga a un canto total de 35 cm. E1d En realidad, la conclusión anterior tiene trampa, porque si recalculamos la viga con canto 35 cm nos saldrá un armado mayor y no cumplirá la relación L/d. Veámoslo: tomamos una viga 25×35 con un flector de 122 m·kN. Sale un armado de 1064 mm², que supone una cuantía de 0,0122 y una relación L/d=14,7, es decir, exige un canto útil de 340 mm y por lo tanto no es suficiente con el canto total de 35 cm... Habría que calcular flecha... E1e Pasamos a un caso más serio, yo diría que incluso preocupante, que evidencia la prudencia con la que hay que utilizar la tabla de la Instrucción. Supongamos la misma viga biapoyada de 5 m de luz y sección 25×40, es decir, CUMPLE la tabla 50.2.2.1.a de EHE-08 si utilizamos la columna de elementos fuertemente armados, que exige una relación L/d=14. Supongamos que sobre la viga carga un forjado con un ancho de banda de 6,00 m, con un peso propio (incluyendo repercusión de peso propio de vigas, peso propio del forjado y peso propio de otros elementos constructivos) de 6,15 kN/m² y sobrecarga de 3,00 kN/m², es decir, un carga combinada de 12,80 kN/m², que en el ancho de banda de 6,00 m antes citado supone una carga total sobre la viga de 76,82 kN/m. Calculamos el flector positivo para la viga isostática y sale 240 m·kN. La armadura NECESARIA de tracción es de 2032 mm² (se cubre con ¡5ø25!), lo que supone una cuantía de 0,0203, bastante superior a la cuantía de 0,015 que la tabla toma como referencia para elementos fuertemente armados. Aplicando las fórmulas de los comentarios de EHE-08 obtenemos que L/d=K·13,2; dado que K=1 (tabla 50.2.2.1.a), es obvio que L/d=13,2. Esta esbeltez, inferior a la de la columna de elementos fuertemente armados de la tabla, exige un canto útil de 378 mm, de modo que no es suficiente con el canto total de 40 cm. Por lo tanto, la viga NO ESTARÍA EXENTA DE LA COMPROBACIÓN DE FLECHA.

El cálculo de flechas

Aplicar las limitaciones de esbeltez nos permite calcular la obra rápidamente con una probabilidad muy baja de problemas por flecha y una garantía de cumplimiento de normativa. Sin embargo, los cantos obtenidos pueden resultar conservadores. Si necesitamos apurar cantos, hay que calcular la flecha de las vigas y forjados para compararla con la flecha admisible. Este proceso implica conocer los diferentes factores que influyen en la flecha: rigidez, fisuración, tiempos de aplicación de cargas, etc. 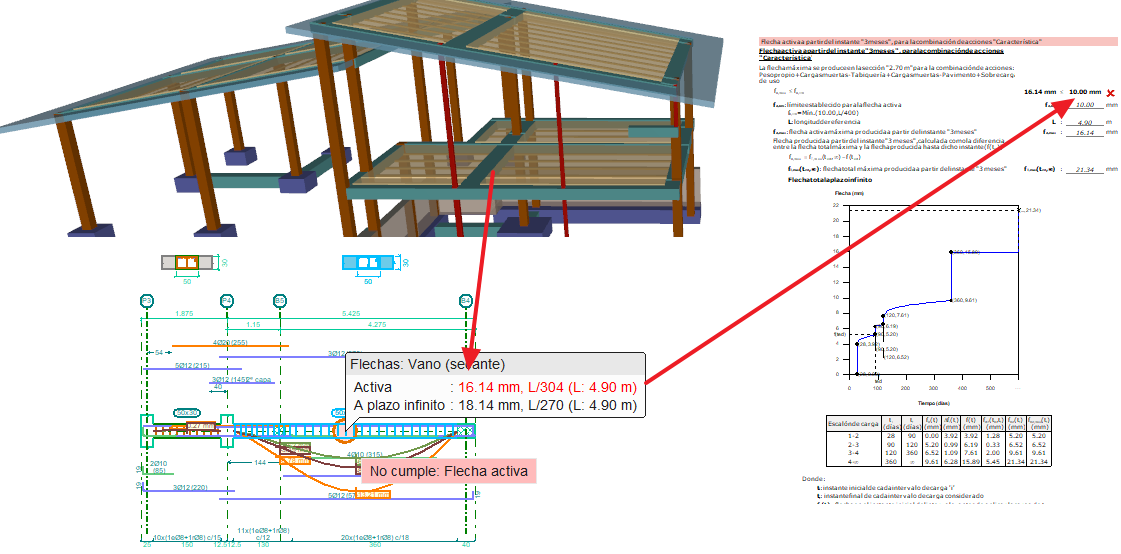Máster Internacional en Estructuras de Edificación con CYPE cálculo de flechas Cypecad nos ofrece el cálculo completo y detallado de la flecha de vigas, pero es nuestro trabajo interpretarlo y, cuando la flecha es excesiva, tomar las medidas correctoras adecuadas.  
J
Autor

Jose Carlos Coya

Co-director del Máster Internacional en Cimentaciones y Estructuras de Contención y el Máster Internacional en Estructuras de Edificación con Cype en Zigurat Global Institute of Technology.
Transform Tomorrow Today
Publicaciones relacionadas