Zigurat Institute of Technology
Blog / BIM & Construction Management
Desenho Generativo com Python e Grasshopper
Categorias

O uso de design generativo é um desafio atual para designers, arquitetos e urbanistas, uma vez que a maioria dos currículos para formar esses profissionais não inclui o pensamento algorítmico. No entanto, o uso de algoritmos é frequentemente a melhor opção para a concepção de projetos paramétricos complexos, pois é necessário reunir muitas formas diferentes para atingir uma composição formal total. Este artigo tem como objetivo apresentar um caso de estudo do uso utilizando linguagens de programação textual e visual (utilizando Python e Grasshopper) no design generativo.
A modelagem paramétrica, também conhecida como modelagem relacional ou design variacional, é uma técnica baseada na utilização de algoritmos paramétricos para projetar modelos virtuais (FIORITO, 2016. MONEDERO, 2000). Ao alterar os valores dos parâmetros do algoritmo, é possível gerar vários projetos diferentes (STAVRIC; MARINA, 2011). Isso é útil quando o modelo precisa ser alterado com frequência durante o processo de design (MYUNG; HAN, 2001), por exemplo, para a criação de formas livres destinadas a serem fabricadas com a ajuda de máquinas de manufatura digital (CELANI; VAZ, 2012). O design algorítmico é frequentemente a melhor opção para a concepção de projetos paramétricos complexos. Apesar de sua reconhecida importância, o design algorítmico é atualmente um desafio para designers, arquitetos e urbanistas, por ser uma disciplina cujo ensino ainda não está difundido nos currículos desses profissionais. Além disso, para usar o projeto algorítmico, é necessário ser capaz de implementar algoritmos em uma dada linguagem de programação. Neste artigo, descrevemos um experimento baseado na implementação de um exemplo prático de modelagem paramétrica. Trata da aquisição de conhecimento que ocorre quando novos conceitos e métodos são adicionados e novas habilidades são assimiladas e relacionadas com outros construtos (DIBELLA, A. J.; NEVIS, 1999). Conhecimento é a adequação do sujeito ao objeto (GAVIRA, 2003). “Há também a suposição implícita de que as habilidades intelectuais adquiridas durante um curso de estudo podem ser transferidas para outras situações que podem ocorrer em um local muito distante e um pouco distante da situação original de aprendizagem”. (LAUDER; REYNOLDS; ANGUS, 1999, p. 480). Recorreu-se ao uso de Python + Khepri como linguagens de programação textual (TPL). Python é uma linguagem de programação projetada para ser uma linguagem de alto nível que facilita o processo de aprendizagem, principalmente para iniciantes (ROSSUM, 1999. VILLARES; MOREIRA, 2017). Python é a linguagem freeware mais utilizada atualmente, de acordo com o ranking IEEE Spectrum (DIAKOPOULO, NICK; CASS, 2017). Sua sintaxe é simples, intuitiva e limpa, e a maioria das implementações Python vem com um loop read-eval-print (REPL) que permite ao usuário experimentar interativamente a linguagem, tornando-a amigável e fácil de aprender. Por fim, muitos pacotes de software CAD e de modelagem 3D incorporam Python como linguagem de script (VILLARES; MOREIRA, 2017). Khepri é uma camada de modelagem arquitetônica pedagógica que abstrai diferentes ferramentas de design auxiliado por computador, como AutoCAD e Rhino 3D e, assim, facilita o uso de Python para fins de design. Como linguagem de programação visual (VPL), usou-se Grasshopper + Anemone. Grasshopper é uma ferramenta de modelagem algorítmica baseada em uma linguagem de programação visual. Isso permite que usuários que não têm conhecimento de programação desenvolvam programas combinando graficamente diferentes componentes em um fluxo de trabalho. Funciona como um plugin do Rhinoceros e é amplamente adotado em escritórios que trabalham com design paramétrico (BUENO, 2016). Os recursos paramétricos do Grasshopper permitem a geração e modificação do projeto simplesmente alterando os parâmetros, evitando a necessidade de reescrever quantidades substanciais de código (OXMAN, 2017). Anemone (ZWIERZYCKI, n.d.) é um plug-in gratuito do Grasshopper que permite ao usuário criar loops com dois componentes dentro do fluxo de trabalho.
Pensamento Computacional
O termo Pensamento Computacional foi usado pela primeira vez por Seymour Papert, que estava desenvolvendo uma abordagem pedagógica para ensinar às crianças essa forma particular de pensar (PAPERT, 1980). O Pensamento Computacional é uma forma de pensamento analítico que, de uma forma geral, pode ser aplicada para resolver qualquer problema (solucionável). Se o pensamento computacional pode ser usado por qualquer pessoa em qualquer situação, ele também deve ser aplicável para resolver o mesmo problema computacional por meio de diferentes linguagens de programação. O uso do pensamento computacional é dividido em três aspectos principais: Abstração, Automação e Análise (WING, 2008). Veja a figura 1 abaixo 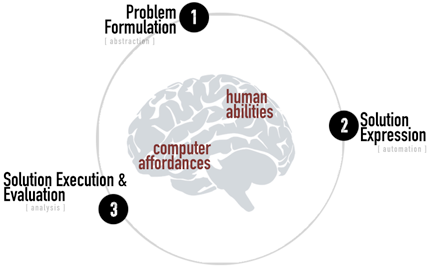 Figura 1 - Procedimentos de pensamento computacional. Fonte: Autor. Abstração é o processo de generalizar a partir de instâncias específicas, removendo detalhes desnecessários, para ajudar a formular o problema a ser resolvido (LEE et al., 2011. WING, 2008). Para tanto, precisamos reconhecer os padrões e parâmetros do problema para que possamos decompô-lo, dividindo as ações repetitivas necessárias para resolver o problema complexo em outras menores e gerenciáveis. A automação da abstração envolve revelar as instruções passo a passo de como fazer algo (WING, 2008). Neste caso de papel, isso envolve instruir um computador codificando o algoritmo necessário que recebe a entrada e produz a saída desejada. A análise é o momento de avaliar se o resultado final corresponde às expectativas em relação aos dados gerados, modelos e outros (LEE et al., 2011. WING, 2008). Se os resultados foram negativos também é hora de avaliar se as abstrações iniciais foram corretas, se fatores importantes foram deixados de fora, se houve situações que não foram consideradas, etc. (LEE et al., 2011).
Figura 1 - Procedimentos de pensamento computacional. Fonte: Autor. Abstração é o processo de generalizar a partir de instâncias específicas, removendo detalhes desnecessários, para ajudar a formular o problema a ser resolvido (LEE et al., 2011. WING, 2008). Para tanto, precisamos reconhecer os padrões e parâmetros do problema para que possamos decompô-lo, dividindo as ações repetitivas necessárias para resolver o problema complexo em outras menores e gerenciáveis. A automação da abstração envolve revelar as instruções passo a passo de como fazer algo (WING, 2008). Neste caso de papel, isso envolve instruir um computador codificando o algoritmo necessário que recebe a entrada e produz a saída desejada. A análise é o momento de avaliar se o resultado final corresponde às expectativas em relação aos dados gerados, modelos e outros (LEE et al., 2011. WING, 2008). Se os resultados foram negativos também é hora de avaliar se as abstrações iniciais foram corretas, se fatores importantes foram deixados de fora, se houve situações que não foram consideradas, etc. (LEE et al., 2011).
Aquisição de conhecimento
Durante uma investigação realizada em 2017 nas aulas de programação para arquitetos em Portugal, descobrimos que a matéria que os alunos consideraram mais difícil de compreender eram as “funções”, nomeadamente as funções recursivas (PONTES, THIAGO BESSA; MIRANDA, GUILHERMINA LOBATO; SANTOS, 2016). Essa é a principal razão pela qual decidimos escolher um exemplo recursivo para fazer este experimento. A segunda razão é que a maioria dos problemas pode ser resolvida por recursão. Uma terceira razão é que a recursão é um conceito que, com alguma criatividade, pode caber em todas as escalas, incluindo Design, Arquitetura e Urbanismo.
Abstração
Usando este primeiro processo de pensamento computacional, definimos nossa tarefa principal: projetar um modelo paramétrico em forma de pirâmide. A próxima tarefa é projetar outro esboço que represente o modelo. Depois disso é possível decompor o problema, entender quais são as partes repetitivas e os parâmetros que precisamos gerenciar (Figura 2). 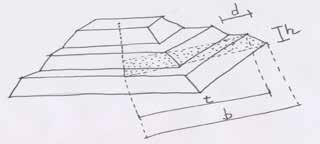 Figura 2 - Desenho de um tronco de pirâmide regular. Durante os primeiros esboços, descobrimos que cada degrau da pirâmide é um tronco piramidal regular. Decompondo esse problema, ficou claro que a primeira coisa que tivemos que fazer para decompor o problema foi projetar um degrau da pirâmide, colocando uma pirâmide menor no topo deste primeiro degrau. Repetindo essa lógica até atingir uma pirâmide de zero degraus podemos gerar a pirâmide inteira. As variáveis identificadas para a primeira etapa foram (Figura 3): P = ponto central da base b = raio da base inferior t = raio da base superior h = altura do degrau s = números laterais de polígonos
Figura 2 - Desenho de um tronco de pirâmide regular. Durante os primeiros esboços, descobrimos que cada degrau da pirâmide é um tronco piramidal regular. Decompondo esse problema, ficou claro que a primeira coisa que tivemos que fazer para decompor o problema foi projetar um degrau da pirâmide, colocando uma pirâmide menor no topo deste primeiro degrau. Repetindo essa lógica até atingir uma pirâmide de zero degraus podemos gerar a pirâmide inteira. As variáveis identificadas para a primeira etapa foram (Figura 3): P = ponto central da base b = raio da base inferior t = raio da base superior h = altura do degrau s = números laterais de polígonos 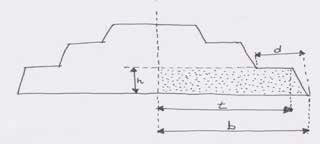 Figura 3 - Desenho de um tronco de pirâmide regular.
Figura 3 - Desenho de um tronco de pirâmide regular.
Automação
Para o processo de automação, uma função recursiva foi adotada. A recursão é uma estrutura de controle fundamental onde uma função chama a si mesma. (Martins, 2015) Os dados do Grasshopper são configurados da esquerda para a direita, consequentemente, não é possível criar recursão no Grasshopper por si só (TEDESCHI; WIRZ; ANDREANI, 2014). Para inserir recursão no Grasshopper, temos que baixar um componente Python Script e inserir um fragmento de linguagem textual no fluxo de trabalho. Porém, como não foi nossa intenção misturar linguagens neste estudo, optou-se por substituir a recursão por uma instrução em loop, desde que possam ser análogas e atingir os mesmos resultados em casos particulares como estes. O loop repete a execução de uma série de instruções por um determinado número de vezes (MARTINS, 2015). Para fazer loops no Grasshopper, existem alguns complementos gratuitos que fornecem componentes especiais para criar um loop, por exemplo, Hoopsnake ou Anemone. Utilizamos o Anemone. O Anemone apresenta dois componentes que devem ser conectados: início do loop e término do loop (Figura 5). Ele funciona substituindo um parâmetro de entrada do “loop começa” por uma saída do “loop termina” um certo número de vezes escolhido pelo usuário. Nas figuras 4 e 5, há uma função recursiva em TPL e um loop em VPL projetando as etapas restantes da pirâmide. Na figura 4 está a definição da função “degrau-pirâmide” e suas variáveis: se o número de degraus dados for igual a zero, não fazemos nada, caso contrário, criamos um degrau e chamamos essas funções do número de degraus. 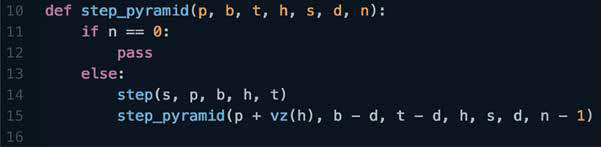 Figura 4 – Recursão em TPL. Fonte: Autor.
Figura 4 – Recursão em TPL. Fonte: Autor. 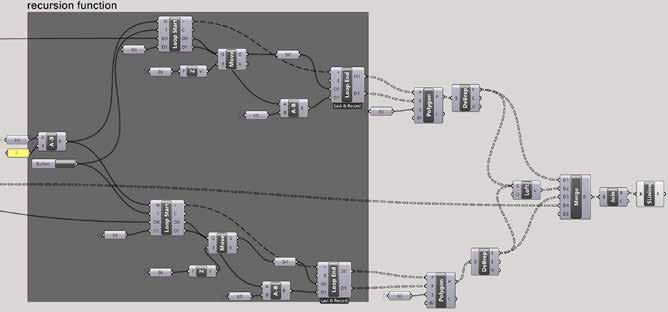 Figura 5 - Loop em VPL. Fonte: Autor.
Figura 5 - Loop em VPL. Fonte: Autor.
Scripts finais
Script final VPL
A lógica do Grasshopper funciona como uma sequência de comandos que flui pelas caixas de componentes da esquerda para a direita. Para facilitar o entendimento, é possível evidenciar que uma coleção específica de componentes está trabalhando em conjunto para gerar um resultado final específico, criando grupos coloridos e rabiscando comentários informativos. Lendo esse script (Figura 6) à esquerda, vemos um grande quadrado cinza com todas as variáveis do modelo (parâmetros). O próximo grande quadrado amarelo refere-se ao desenho da primeira etapa. O laranja se refere aos polígonos superior e inferior e, fora desse quadrado, os componentes se unem e elevam as partes desta etapa. O quadrado cinza apresenta as ações repetitivas para gerar as outras etapas. Logo após o último quadrado, estão os componentes para unir e elevar o modelo da pirâmide de degraus de furo. Organizando o roteiro com cores e textos fica fácil entender as intenções de cada grupo de ações. Na maioria dos casos, outros usuários precisam apenas alterar as variáveis / parâmetros e são fáceis de encontrar dessa forma, por exemplo. No entanto, como o script está se tornando complexo, é difícil ler todas as intenções dos componentes e suas conexões. 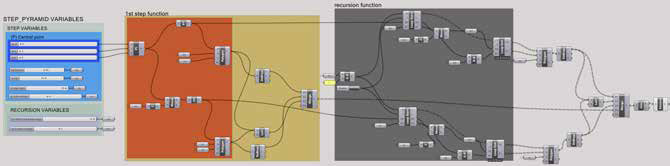 Figura 6 – Script final em VPL. Fonte: Autor.
Figura 6 – Script final em VPL. Fonte: Autor.
Script final TPL
Para um iniciante em uma Linguagem de Programação Textual, é possível que seja difícil entender cada linha do script, mas com a prática isso se torna mais fácil. O último passo para desenhar a pirâmide é chamar a função step_pyramid (p, b, t, h, s, d, n), mas desta vez inserindo valores absolutos nos parâmetros. Por exemplo: P = ponto central da base = é uma coordenada cartesiana, definida na origem = xyz (0, 0, 0) b = raio da base inferior = valor absoluto = 120 t = raio da base superior = valor absoluto = 115 h = altura do degrau = valor absoluto = 20 d = distâncias horizontais entre etapas = valor absoluto = 15 n = número de etapas = valor absoluto = 6 s = números laterais de polígonos = valor absoluto = 4 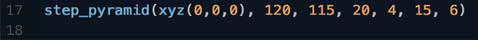 Figura 7 – Chamando a função em TPL. Fonte: Autor.
Figura 7 – Chamando a função em TPL. Fonte: Autor. 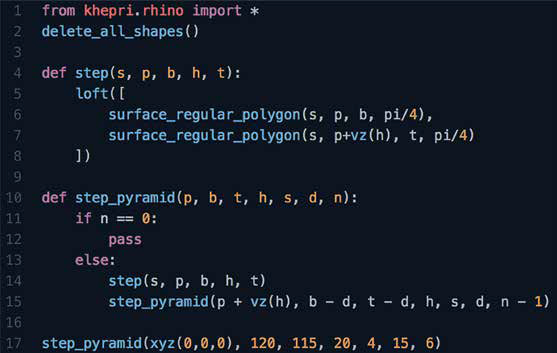 Figura 8 - Script final em TPL. Fonte: Autor.
Figura 8 - Script final em TPL. Fonte: Autor.
Análise
Ao final deste experimento, foi possível obter em ambas as línguas a mesma forma de modelo usando os mesmos números de variáveis (Figura 9). 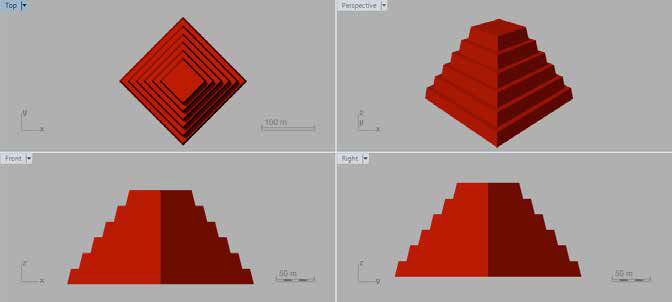 Figura 9 – Modelo Final. Fonte: Autor. Depois que o script foi feito, foram testadas aplicações de diferentes números para gerar várias pirâmides (Fig. 10). Para o TPL era uma questão de alterar a chamada de função e executar, para o VPL basta alterar os controles deslizantes e “assar” o componente final.
Figura 9 – Modelo Final. Fonte: Autor. Depois que o script foi feito, foram testadas aplicações de diferentes números para gerar várias pirâmides (Fig. 10). Para o TPL era uma questão de alterar a chamada de função e executar, para o VPL basta alterar os controles deslizantes e “assar” o componente final. 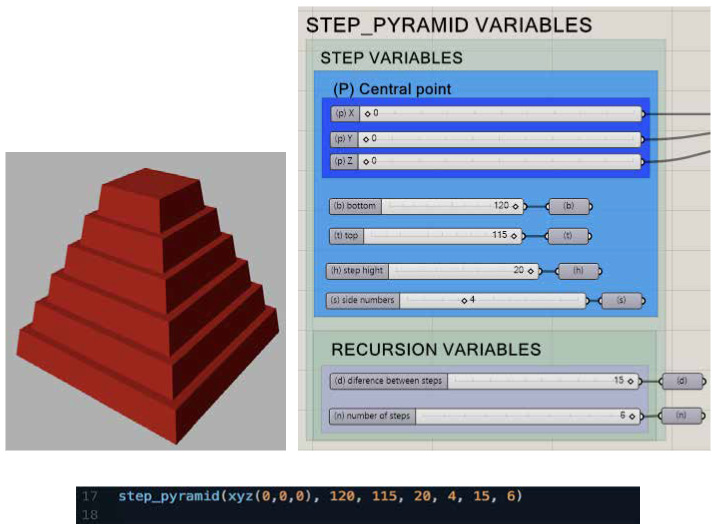 Figura 10 – Formas variadas a partir de diferentes argumentos. Fonte: Autor.
Figura 10 – Formas variadas a partir de diferentes argumentos. Fonte: Autor.
Conclusões
Concluímos que a mesma lógica (pensamento computacional) pode ser aplicada para gerar um modelo paramétrico em linguagem textual e visual. Embora esses resultados dos modelos paramétricos pudessem ser obtidos adotando-se diferentes estratégias de programação, é fato que eles poderiam ser resolvidos por recursão e loop também, tanto em linguagens textuais quanto visuais. Poderíamos gerar o mesmo design em ambas as linguagens. Esperamos que aprender a programar dessa forma facilite a mudança para uma nova linguagem sempre que for necessário. Também foi possível comparar linguagens de programação visual e textual e suas peculiaridades. De acordo com a legibilidade, entendemos que as linguagens de programação textual seriam uma opção melhor do que a linguagem visual. Parece ser mais fácil de ler e compreender o script, porque claramente, se submetermos o script a outras pessoas, elas podem identificar facilmente as ligações entre entradas, instruções e saídas. À medida que o script está se tornando complexo, essas conexões se tornam mais difíceis de identificar na linguagem visual. De acordo com a performance, na linguagem textual também parece ser melhor do que visual. Em nosso experimento, os modelos generativos foram projetados de forma mais rápida, no mesmo ambiente, executando o Python Script, depois no Grasshopper. Por outro lado, é mais fácil para o programador conceber o script no Grasshopper. Eles podem ver os resultados da modelagem em tempo real para cada conexão feita. Ele permite que eles identifiquem possíveis acertos e erros durante o processo. Como o script é baseado no esquema de workflow, também é fácil desenvolver o script de acordo com as primeiras abstrações do problema. Ambas as línguas têm ativa comunidade online e rica documentação gratuita que pode ajudar a resolver dúvidas e o processo de aprendizagem.
Quer dominar Python, Grasshopper e o pensamento computacional aplicado ao design?
Com o Master em Inteligência Artificial para Arquitetura e Construção da Zigurat, você transforma código em criatividade.
Referências
BUENO, E. Grasshopper. In GASPAR, J.; BRAIDA, F.; LIMA, F.; FONSCECA, J.; MORAIS, V. R. R. (Orgs.) 101 conceitos de arquitetura e urbanismo na era digital. p. 118 – 119. Sao Paulo: ProBooks, 2016. CELANI, M. G. C.; VAZ, C. E. CAD scripting and visual parametric modeling environments: a comparison from a pedagogical point of view. In: Cadernos PROARQ, 18., 177–194, 2012. DIAKOPOULO, N.; CASSS. (2017). Interactive: The Top Programming Languages 2017. Avaiable in: <https://spectrum.ieee.org/static/interactive-the-top-programming-languages-2017> DIBELA, A. J.; NEVIS, E. C. Como as organizações aprendem: uma estratégia integrada voltada para a construção da capacidade e aprendizagem. São Paulo: Ed. Educator, 1999. FIORITO, W. Modelagem paramétrica. In: GASPAR, J.; BRAIDA, F.; LIA, F.; FONSCECA, J.; MORAIS, V. R. R. (Orgs.), 101 conceitos de arquitetura e urbanismo na era digital. p. 139–140. Sao Paulo: ProBooks, 2016. GAVIR A, M. O. Simulação Computacional como uma ferramenta de aquisição de conhecimento. 2003. LAUDER, W.; REYNOLDS, W.; ANGUS, N. Transfer of knowledge and skills: Some implications for nursing and nurse education. In: Nurse Education Today, 19(6), p. 480–487, 1999. LEE, I.; MARTIN, F.; DENNER, J.; COULTER, B.; ALLAN, W.; ERIC KSON, J.; WERNER, L. (2011). Computational thinking for youth in practice. ACM Inroads, 2(1), 32. https://doi.org/10.1145/1929887.1929902 MARTINS, J. P. Programação em Python. Introdução à Programação Utilizando Múltiplos Paradigmas. (P. Lourtie, Ed.) (1st ed.). Lisboa: IST Press, 2015. MONEDERO, J. Parametric design: a review and some experiences. In: Automation in Construction, 9(4), 369-377, 2000. MYUNG, S.; HAN, S. Knowledge-based parametric design of mechanical products based on configuration design method. In: Expert Systems with Applications, 21(2), 99–107, 2001. PAPERT, S. Mindstorms: Children, computers and powerful ideas. New Ideas in Psychology (Vol. 1). New York: Basic Books, 1980. PONTES, T. B.; MIRANDA, G. L.; SANTOS, D. M. A programação de computadores para alunos de arquitectura: uma análise do uso da linguagem Racket para protótipos 3d. In: Digital Technologies & Future School (Vol. 2016, p. 1206). Lisbon: Instituto de Educação da Universidade de Lisboa. ROSSUM, G. van. (1999). Computer Programming for Everybody. Retrieved from https://www.python.org/doc/essays/cp4e/ STAVRIC, M.; MARINA, O. Parametric Modeling for Advanced Architecture. In: International Journal of Applied Mathematics and Informatics, 5(1), p. 9–16, 2011. TEDESCHI, A. AAD_Algorithms-Aided Design: Parametric Strategies Using Grasshopper, Le Penseur, Italy, 2014. VILLARES, A. B. do A.; MOREIRA, D. de C. (2017). Python on the Landscape of Programming Tools for Design and Architectural Education (pp. 207–211). São Paulo: Blucher. https://doi.org/10.5151/sigradi2017-033 WING, J. M. (2008). Computational thinking and thinking about computing. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366(1881), 3717–3725. https://doi.org/10.1098/rsta.2008.0118 ZWIERZYCKI, M. (n.d.). Anemone. Retrieved November 28, 2017, from http://www.food4rhino.com/app/anemone Autor: Thiago Bessa Pontes, professor adjunto da Universidade Federal do Cariri. Professor do Curso de Aperfeiçoamento em Desenho paramétrico com Programação Visual em BIM. Dynamo, Grasshopper e Python.



