Jose Carlos Coya
La presión admisible, ¿es bruta o neta?
Categorias

Cuando calculamos zapatas, una de las comprobaciones principales es el estado límite de hundimiento o capacidad portante. El modelo más general para obtener la presión de hundimiento se basa en los estudios de Prandtl, ampliados por Terzaghi y complementados por diversos autores que fueron añadiendo múltiples correcciones. 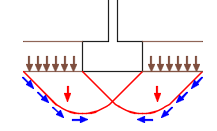 En ocasiones surge la pregunta sobre si la presión de hundimiento así obtenida se debe comparar con la presión bruta o con la presión neta de la cimentación. Para averiguarlo, veamos un ejemplo llevando el modelo al límite: supongamos un terreno sin cohesión y con un ángulo de rozamiento casi nulo (si fuese nulo, sería un líquido). ¿Cuál es su presión de hundimiento o capacidad portante? Para simplificar la formulación usamos la expresión de Terzaghi, más manejable porque no incluye los coeficientes de profundidad, forma, inclinación o presencia de taludes, que aquí no nos aportan nada.
En ocasiones surge la pregunta sobre si la presión de hundimiento así obtenida se debe comparar con la presión bruta o con la presión neta de la cimentación. Para averiguarlo, veamos un ejemplo llevando el modelo al límite: supongamos un terreno sin cohesión y con un ángulo de rozamiento casi nulo (si fuese nulo, sería un líquido). ¿Cuál es su presión de hundimiento o capacidad portante? Para simplificar la formulación usamos la expresión de Terzaghi, más manejable porque no incluye los coeficientes de profundidad, forma, inclinación o presencia de taludes, que aquí no nos aportan nada.  Al ser la cohesión nula, el primer sumando se anula.
Al ser la cohesión nula, el primer sumando se anula. 
Al ser el ángulo de rozamiento prácticamente nulo, Ng tiene un valor ínfimo y por tanto podemos anular también el último sumando, con lo que nos queda

Al ser el ángulo de rozamiento prácticamente nulo, el factor de sobrecarga Nq tiene valor prácticamente 1. 
Salvo que tengamos una carga adicional fuera de la zapata, que resultaría favorable, el valor de q0k es igual al peso del terreno circundante. 
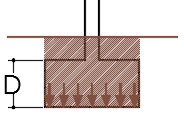
Dicho de otra manera, la presión de hundimiento es igual a la presión de la tierra que hemos quitado.
Podemos entonces deducir que la fórmula de hundimiento o capacidad portante nos da un valor de presión bruta, no de presión neta.
Por ejemplo, supongamos una zapata de 2 m de ancho cimentada a 1 m de profundidad en un terreno con peso específico 20 kN/m³. Hemos excavado 1 m, por lo que la presión que hemos restado es 20 kN/m².
Calculamos la presión de hundimiento y obtenemos 20 kN/m².
Por lo tanto, podemos colocar ahí una zapata que transmita 20 kN/m², no 20 kN/m² más el peso de tierras, es decir, el valor de 20 kN/m² que nos da la fórmula es un valor de presión bruta.
Aplicación de los coeficientes de seguridad
Hasta aquí hemos trabajado sin aplicar coeficientes de seguridad. Si en el caso anterior aplicamos un coeficiente de seguridad de 3, nos encontraremos con que el terreno aguanta malamente un tercio de su propio peso, algo totalmente absurdo. Esto nos lleva a una aplicación más afinada del coeficiente de seguridad, que consiste en aplicar el coeficiente solamente a la presión que excede la debida al peso propio de las tierras en lugar de hacerlo a la presión total.

Donde:
qadm Presión admisible
qhund Presión de hundimiento bruta, obtenida de la fórmula de hundimiento
qter Presión del terreno antes de la excavación, es decir, la debida al peso propio del suelo excavado
En el ejemplo anterior, esta consideración mantendría la presión admisible en 20 kN/m².
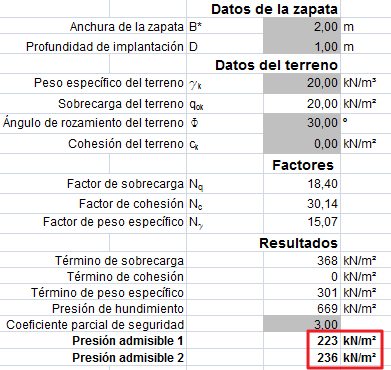
Veamos un ejemplo más realista. Supongamos la misma zapata 2 m de ancho cimentada a una profundidad de 1 m, ahora en un suelo granular con ø=30º y g=20 kN/m³.
La presión de hundimiento es 669 kPa.
Aplicando sin más un coeficiente de seguridad 3 obtenemos una presión admisible 669/3=223 kPa.
Probamos ahora a no aplicar el coeficiente de seguridad al peso propio del terreno excavado. La presión de dicho terreno es 20×1=20 kPa.
Por lo tanto: 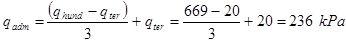
Vemos que el valor es mayor, aunque la diferencia es escasa, por lo que es habitual aplicar 3 a todo y no darle más vueltas. En cualquier caso, se trata de una presión a comparar con la presión bruta.
Si recibimos un estudio geotécnico que nos dice que la presión admisible es 223 KPa y la tomamos como neta, estamos admitiendo cargar 20 kPa de más. Considerando que podíamos aumentar hasta 236 kPa manteniendo el cálculo riguroso, vemos que en la práctica la diferencia no es significativa.
Ahora bien, ¿qué ocurre en el caso de un pozo de cimentación o una losa de sótano, donde la profundidad es claramente mayor?
Vemos que el valor es mayor, aunque la diferencia es escasa, por lo que es habitual aplicar 3 a todo y no darle más vueltas. En cualquier caso, se trata de una presión a comparar con la presión bruta.
Si recibimos un estudio geotécnico que nos dice que la presión admisible es 223 KPa y la tomamos como neta, estamos admitiendo cargar 20 kPa de más. Considerando que podíamos aumentar hasta 236 kPa manteniendo el cálculo riguroso, vemos que en la práctica la diferencia no es significativa.
Ahora bien, ¿qué ocurre en el caso de un pozo de cimentación o una losa de sótano, donde la profundidad es claramente mayor?
Pozos
Por su mayor profundidad, un pozo supone restar una presión de tierra mayor que en el caso de zapatas. Con un terreno de 20 kN/m², excavar 4 m supone restar 80 kN/m². Ahora bien, el mismo incremento de profundidad hace que aumente el término de sobrecarga y con ello la capacidad portante sea mucho mayor.
En el ejemplo anterior, si simplemente aumentamos la profundidad de implantación a 4 m, la capacidad portante asciende a 1773 kN/m² aún aplicando la misma formulación, sin considerar otros efectos favorables como el rozamiento lateral o la resistencia a cortante del terreno por encima del nivel de implantación
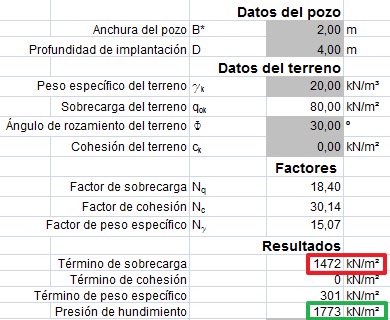
Ante este panorama los 80 kN/m² de la excavación son poco relevantes.
Losas de sótano
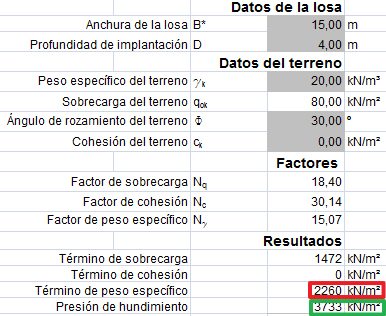
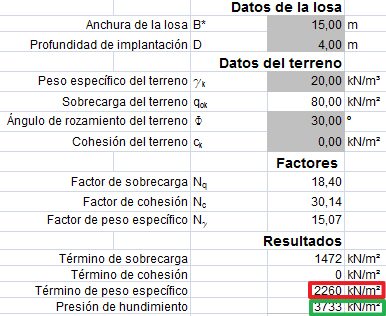
En el caso de losas, además de la profundidad, el ancho es también también mayor, lo que hace aumentar el término de peso específico. En el ejemplo anterior, si simplemente aumentamos el ancho a 15 m, la presión de hundimiento asciende a 3733 kN/m², los 80 kN/m² son aún menos relevantes.
Conclusiones
De los ejemplos anteriores podemos deducir que la presión que nos da el modelo de capacidad portante es conceptualmente una presión bruta, pero también que la diferencia entre presión bruta y presión neta es pequeña en zapatas y, aunque es mayor en pozos y losas, resulta menos relevante a efectos prácticos.
https://www.youtube.com/watch?v=I1tqZ8rCH70
Este artículo está relacionado con el Curso de Posgrado en Cimentaciones Profundas y Estructuras de Contención.
Formación relacionada