Categorias
El edificio es un sistema en el que todo está conectado, cada elemento forma parte de un conjunto. Para abordar su complejidad, podemos pensarlo como un conjunto de subsistemas más o menos especializados: sistema estructural, sistema envolvente, sistema de compartimentación, sistema de acabados, sistema de acondicionamiento, sistemas de servicios... pero no deja de ser uno, por lo que la resolución de cada sistema no puede basarse únicamente en su propia optimización, sino ser óptima para el conjunto del edificio.
El edificio es uno y la estructura es una parte inseparable de esa unidad. Llamamos estructura al elemento o conjunto de elementos capaces de resistir su propio peso y las acciones exteriores y transmitirlas al terreno. Estos elementos pueden tener o no otras funciones. Por ejemplo, en obras de albañilería o de concreto, los muros portantes, además de sostener los elementos de piso y cubierta, forman parte del cerramiento; las cúpulas y bóvedas de piedra o ladrillo y las losas de hormigón forman la propia cubierta de muchos edificios. En otros muchos casos la estructura está formada por elementos específicos cuya misión es únicamente sostener los elementos de cubierta y cerramiento, como apuntaban las bóvedas de crucería góticas. Sin embargo, aunque todavía se usan en algunos casos muros portantes, la mayoría de los edificios actuales tienen un esqueleto estructural formado por barras de hormigón, acero o madera que sostienen elementos sin misión portante específica, más allá de transmitir a dicho esqueleto las acciones que reciban directamente. El esqueleto habitual de los edificios actuales consiste en soportes verticales y vigas horizontales o inclinadas que reciben las acciones de los cerramientos, los forjados y las cubiertas.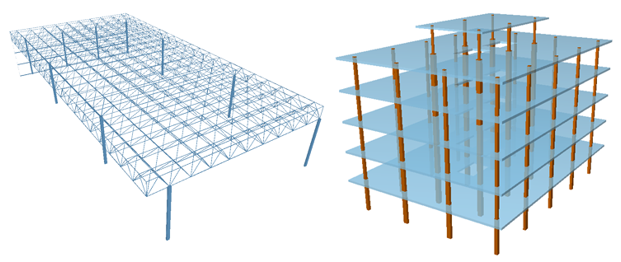 
Elementos estructurales en una nave y en un edificio de pisos
Antiguamente la estructura de los edificios se dimensionaba empíricamente, en base a la experiencia previa. De ello surgieron reglas básicas de cálculo, muchas de ellas simplemente geométricas y referidas a proporciones. A partir del Renacimiento, el espíritu científico y tecnológico, con el consiguiente desarrollo de las matemáticas y la física, permitieron simplificar las estructuras en forma de modelos resolubles con los métodos disponibles en cada época. El análisis de la estructura real es inabordable incluso con los más sofisticados métodos actuales de simulación, es preciso trabajar siempre sobre un modelo matemático cuya complejidad, dentro de las posibilidades de los medios disponibles, debe ser proporcional al problema a resolver. Al final, el modelo es lo que calculamos, por lo que el resultado depende de su correcta elección y adecuación a la realidad. Los métodos de resolución pueden ser más o menos precisos, pero la correspondencia entre los resultados obtenidos y el comportamiento real de la estructura no será mayor que la correspondencia entre el modelo y la estructura real. El modelo debe incluir los siguientes aspectos:
Las estructuras son siempre tridimensionales, todos sus elementos tienen volumen. Sin embargo, el análisis de volúmenes es muy complejo. Además, en estructuras de edificación los elementos suelen tener una o dos dimensiones claramente superiores a la tercera, por lo que es habitual reducirlos a superficies o a barras. La mayoría de las estructuras de edificación se pueden asimilar, de una u otra manera, a barras con una sección generatriz que define sus propiedades (inercia, área...). Si se trata de una estructura en la que los elementos son claramente lineales, el modelo es evidente. Por ejemplo, podemos modelar la estructura de un columpio.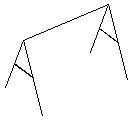 
Columpio Generalmente las edificaciones tienen superficies que definen los volúmenes: cerramientos y cubiertas. Estas superficies pueden introducirse o no en el modelo. Por ejemplo, supongamos la siguiente estructura, simplemente cuatro pilares y una losa. 
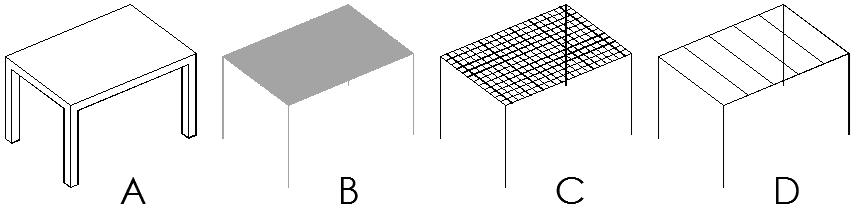La figura A representa un modelo con elementos tridimensionales. Podría ser el más aproximado a la realidad. Existen programas que permiten modelarlo y analizarlo, pero resulta poco operativo. En la figura B las barras están modeladas como barras la losa está modelada como una lámina. Es un modelo muy habitual en los programas actuales, con elementos finitos. La figura C muestra un modelo similar, pero la losa está simulada con barras formando un entramado. La figura D muestra un tipo de losa diferente, podría ser el caso de una losa nervada unidireccional o una cubierta con correas de acero o madera, las vigas y viguetas/correas están modeladas como barras. Los modelos pueden reflejar la estructura completa o dividirla en partes más abordables. Por ejemplo, en el caso de una cubierta con correas, es habitual analizar por un lado las correas y por otro lado la estructura de soportes y dinteles.
En un edificio de pisos, una opción es analizar primero el forjado, tomando una vigueta representativa, en un tramo o en varios consecutivos, y analizarla independientemente, como un modelo unidimensional. 
Modelo de cálculo de vigueta Continuando el ejemplo, tradicionalmente el cálculo del edificio continuaba con un modelo de un pórtico plano, formado por pilares y vigas alienados.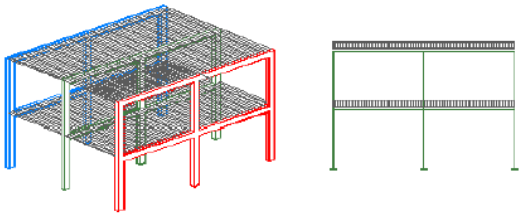 
Modelo de cálculo de pórtico La ventaja de los modelos bidimensionales es su sencillez, ya que pueden ser analizados con métodos manuales o métodos informáticos sencillos. Actualmente su utilidad se limita a los análisis simplificados para predimensionados, tanteos o comparativas, ya que hay muchas situaciones que no reflejan adecuadamente. Los pórticos planos funcionan relativamente bien bajo cargas verticales en estructuras muy regulares, con soportes alineados de manera que los pórticos sean efectivamente planos y los forjados trabajan en una misma dirección. Las cosas se complican si los soportes no están alineados, porque los pórticos dejan de ser planos aunque se intenten modelar como tales, además de la complicación constructiva que suponen los nervios de longitud variable. 
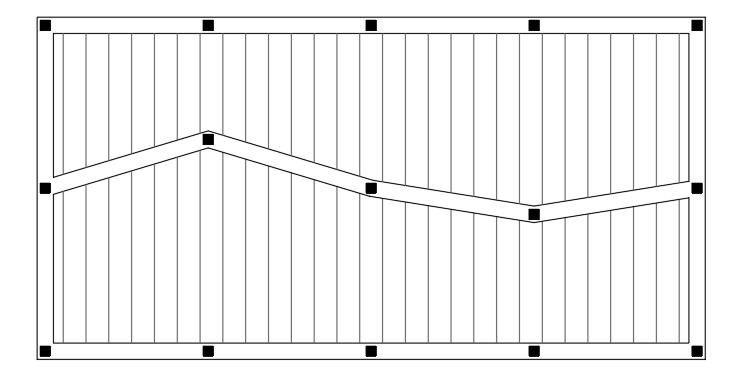Soportes no alineados Si hay forjados en ambas direcciones, aparecen pórticos perpendiculares que interaccionan entre sí. Los soportes reciben cargas de ambos pórticos. 
Forjados en ambas direcciones Bajo cargas horizontales paralelas a los pórticos, no siempre es inmediato el reparto de esfuerzos entre los distintos pórticos, ya que depende de su rigidez.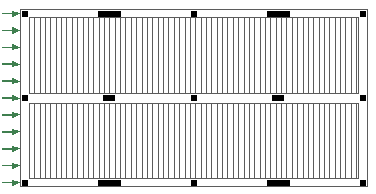 
Soportes de distintas dimensiones Para resistir cargas horizontales importantes perpendiculares a los pórticos de carga es necesario disponer pórticos transversales. 
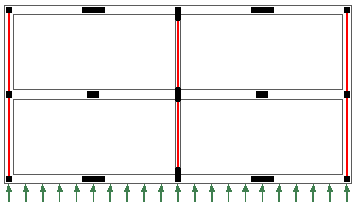Acciones perpendiculares a los pórticos En estructuras regulares hay métodos para considerar estas cuestiones, aceptando simplificaciones que, a poco que aparezcan irregularidades, pueden tornarse inaceptables, a la vez que el esfuerzo de cálculo se multiplica. 
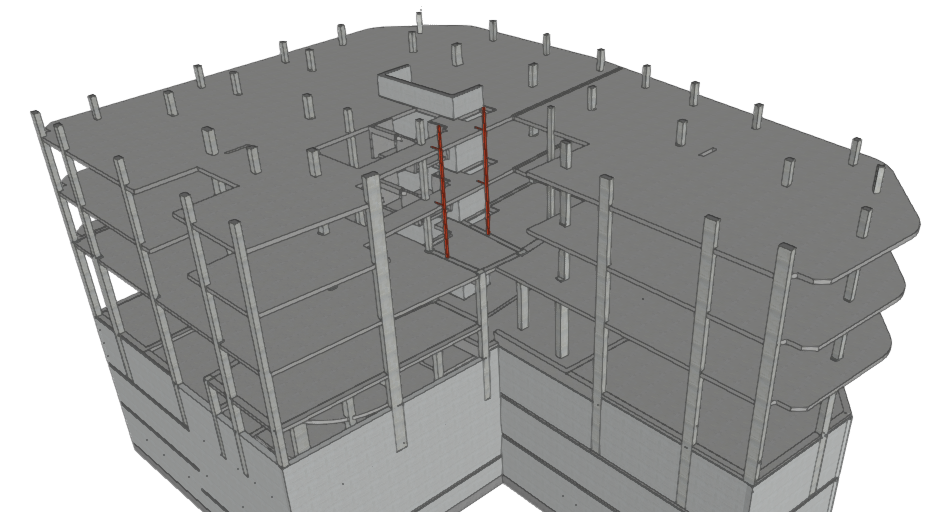Edificio de geometría irregular
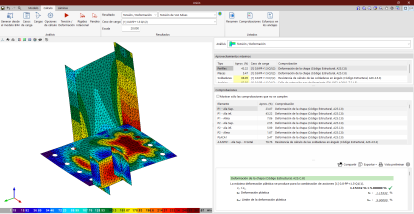
Mucha mayor generalidad presenta el cálculo de pórticos tridimensionales. Resulta inabordable manualmente, pero actualmente se pueden resolver con multitud de programas informáticos.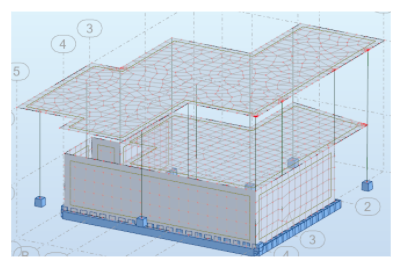 
Modelo tridimensional generado en Autodesk Robot La mayoría de programas de estructuras permite modelar elementos unidimensionales (barras) y elementos bidimensionales (láminas), con diferentes opciones para considerar las propiedades de los elementos, las vinculaciones entre elementos y con el exterior, las excentricidades, las acciones, los comportamientos lineales y no lineales, los efectos del tiempo, etc. 
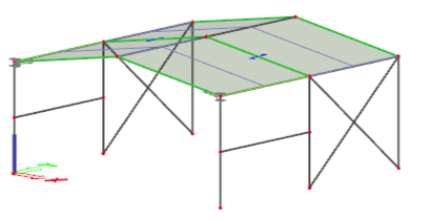Modelo tridimensional generado en Scia Engineer El modelo tridimensional permite considerar la estructura como conjunto y analizar con un solo modelo el comportamiento de la estructura ante acciones verticales y horizontales, en cualquier dirección. A partir de ahí, se abre un nuevo abanico de posibilidades, introduciendo cálculos no lineales, comportamiento dinámico, estudio de inestabilidad, análisis en el tiempo, imperfecciones, etc.
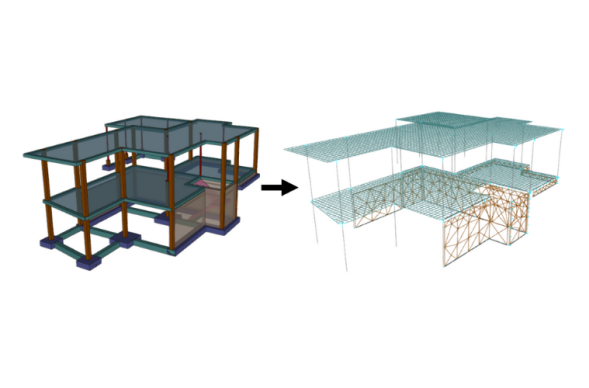
En la mayoría de los programas el modelo de cálculo, también llamado modelo analítico, se introduce directamente, generalmente de manera gráfica. Es el caso, por ejemplo, de Cype3D, Scia, Dlubal RFEM, Autodesk Robot, Midas Gen…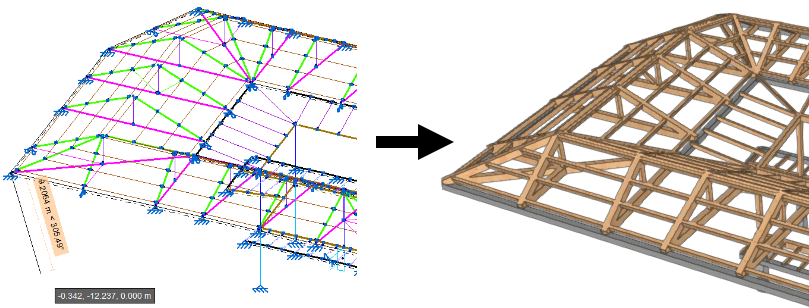 
Introducción directa del modelo analítico y generación del modelo físico en Cype3D A partir del modelo analítico el programa puede generar la volumetría de los elementos constructivos. Por el contrario, en otros programas se modelan los elementos estructurales como tales -pilares, vigas, muros, losas- y el programa genera automáticamente el modelo analítico. Es el caso, por ejemplo, de Cypecad. 
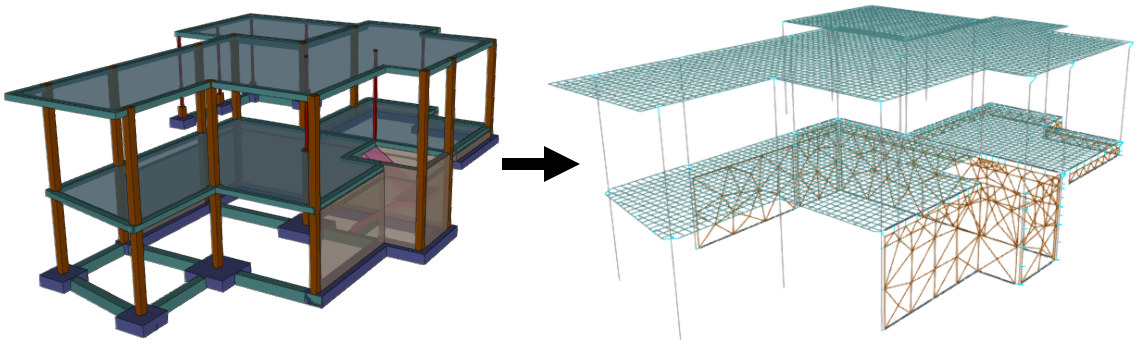Introducción directa del modelo físico y generación del modelo analítico en Cypecad Esta dualidad se traduce también a los caminos de interoperabilidad con modeladores BIM: es posible que el programa de estructuras lea directamente el modelo analítico generado en el modelador BIM o bien que lea el modelo físico y genere internamente el modelo analítico. Obviamente no todas las opciones están disponibles en todos los programas, cada programa tiene sus propios procedimientos. En futuras entradas veremos con más detalle algunas particularidades de algunos programas y procedimientos.
Jose Carlos Coya
Formación relacionada
