Introducción
El diseño óptimo de la superestructura de un puente ejerce una gran influencia sobre el costo total del proyecto, ya que la carga permanente de la superestructura puede ser muy significativa y por ende la magnitud de las cargas gravitacionales que son transmitidas a la infraestructura.
En la actualidad, el uso de nuevos materiales ha permitido el desarrollo de nuevas formas estructurales simples y complejas, y por ende el desarrollo de métodos de análisis, que en algunos casos requieren del uso de teorías matemáticas complejas. De allí que muchas investigaciones han estado orientadas a facilitar los procesos de análisis.
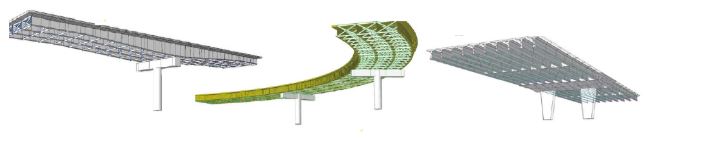
Figura 1: Modelos tridimensionales de puentes.Fuente: MIDAS Information Technology Co.

Figura 2: Modelos de puentes complejos.Fuente: MIDAS Information Technology Co.
El uso de ordenadores ha permitido minimizar la cuantía de cálculos manuales, facilitando el análisis y diseño de estructuras de puentes complejas.
Sin embargo, el profesional dedicado al análisis de este tipo de estructuras debe estar familiarizado con las teorías fundamentales que rigen el comportamiento de estas superestructuras e infraestructuras, con la finalidad de optimizar los procesos incorporados en los sistemas informáticos, y con la finalidad de seleccionar los métodos de modelado, análisis y diseño que sean más óptimos según la geometría propuesta, el sistema estructural involucrado y el comportamiento esperado.
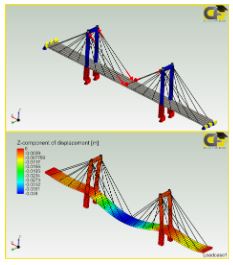
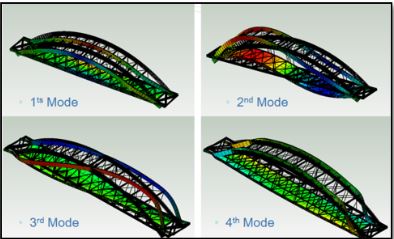
Figura 3: Modelos de puentes atirantados y tipo arco en elemento finito (MEF).
Fuente: CivilFEM Software.
Comportamiento del tablero considerado en los procesos de modelado y análisis
En el análisis estructural de una edificación, por lo general las cargas se consideran que ocupan posiciones fijas, mientras que en los puentes la carga viva o móvil sobre el tablero puede ocupar posiciones variables, tanto longitudinal como transversalmente. Este aspecto representa una de las principales preocupaciones en el análisis y diseño del tablero de un puente. Mediante el uso de líneas de influencia en análisis bidimensionales y mediante superficies de influencia en análisis tridimensionales, es posible representar estos efectos de cargas móviles en las diferentes direcciones de los tableros.

Figura 4: Línea de influencia para diagrama de momento en modelo bidimensional.
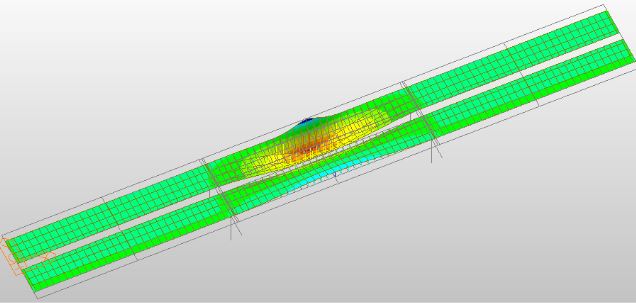
Figura 5: Superficie de influencia para diagrama de momento en modelo tridimensional.
Con la finalidad de comprender el comportamiento que envuelve al tablero de un puente, se puede emplear el siguiente razonamiento físico. Se asume un tablero cargado longitudinalmente mediante un eje de carga.
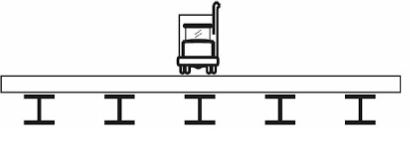
Figura 6: Tablero cargado mediante un eje de carga.
Si dicha carga concentrada se posiciona sobre el tablero directamente sobre una de las vigas, dicha viga soportará una mayor porción de la carga total que las otras paralelas a ella. La losa y todas las vigas experimentaran una flexión longitudinal en el plano que contiene el eje de carga.
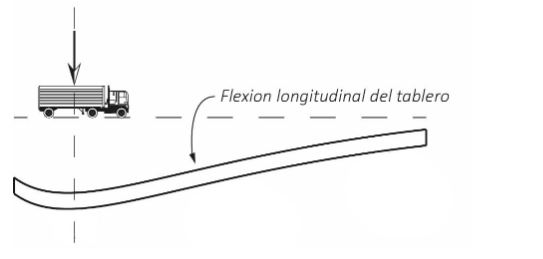
Figura 7: Flexión longitudinal del tablero.
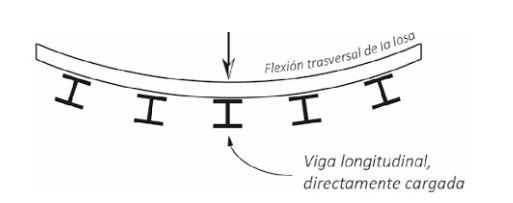
Figura 8: Flexión transversal del tablero.
Adicionalmente, el tablero experimenta una flexión transversal ocasionando que las vigas adyacentes experimenten fenómenos de torsión conjuntamente con el tablero, para mantener la compatibilidad de desplazamientos en la interfase losa-viga. La participación de estas vigas en el comportamiento del tablero dependerá de la rigidez de la losa y del vano, y de las separaciones y rigideces de las vigas. El cálculo de este proceso de participación es conocido como distribución de carga.
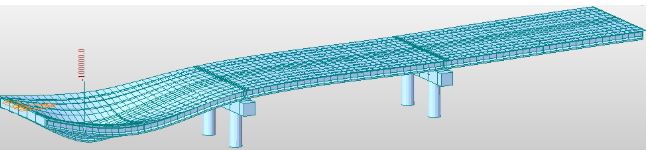
Figura 9: Deformación del tablero en un modelo tridimensional.
En la imagen superior se puede apreciar un modelo tridimensional, que representa de manera aproximada el razonamiento físico descrito previamente. La deformada que presenta el modelo, evidencia la veracidad de lo ya mencionado; sin embargo, la magnitud de la deformación y el comportamiento general del puente dependerán de diversos factores, como por ejemplo la magnitud de la carga, dimensiones de las vigas y la losa, condiciones de apoyo, luces entre apoyos, etc.,
Al comprender este comportamiento podemos entonces evidenciar lo importante que es muchos casos, realizar el análisis de los puentes a partir de modelos tridimensionales, debido a que, además de simular de forma más exacta el comportamiento de la estructura, también se consideran los efectos de la interacción entre los distintos miembros estructurales que la conforman. Sin embargo, sigue siendo muy válido el realizar análisis bidimensionales de manera separada a componentes específicos del puente, como es el caso de la losa del tablero; o bien, la viga que está directamente bajo la carga vehicular, que puede ser analizada mediante un modelo en 2D, debido a que dicha viga no manifestaría los fenómenos de torsión indicados anteriormente y que ocurren en el resto de las vigas.
Métodos de análisis de tableros de puentes
Los métodos de análisis de los tableros de un puente, se pueden clasificar de la siguiente forma:
- Métodos clásicos
- Métodos computacionales
- Métodos simplificados
Entre los principales métodos clásicos se encuentran: el método de la grilla, el método de las chapas y el método de análisis de tableros ortotrópicos equivalentes. Debido a la complejidad matemática de estos métodos, los mismos se consideran como una solución poco eficiente al proceso de análisis de tableros, debido a que los mismos consumen tiempo por exigir cálculos manuales extensos y por lo tanto son poco atractivos en los procesos de elaboración de proyectos. Todo esto ha permitido el desarrollo de los llamados métodos simplificados, tales como el método de los coeficientes de distribución que se encuentra contemplado en el Código AASHTO LRFD.
Ahora bien, mediante el adecuado proceso de discretización y modelado, todo tipo de tablero puede ser analizado mediante el método de elementos finitos. Recientes avances en los métodos computacionales y métodos de análisis numéricos han permitido el desarrollo de diferentes programas o softwares en el área de análisis estructural.
Método de elementos finitos
El método de elementos finitos (FEM por sus siglas en ingles), es una técnica de procesamiento numérico que permite calcular soluciones aproximadas a ecuaciones diferenciales con diferentes condiciones de borde, las cuales pueden estar representadas por los miembros colindantes como, por ejemplo: las cimentaciones, los apoyos de tableros (bearings), el terreno de apoyo, entre otros. El método se fundamenta en dividir el miembro analizado o un determinado medio continuo, en varios elementos de menores dimensiones, conocidos como elementos finitos. La unión entre estos elementos finitos se efectúa en sus puntos nodales, con la finalidad de garantizar la compatibilidad de deformaciones entre los elementos adyacentes conectados, garantizando además que éstos posean los mismos grados de libertad. El desplazamiento de cada nodo puede ser determinado mediante un conjunto de ecuaciones algebraicas simultáneas; y a través de relaciones de compatibilidad que facilitan los procesos de interpolación, se obtienen las deformaciones o desplazamientos del resto de la estructura.
Los elementos finitos, desde el punto de vista matemático se definirán con características ideales en función de los miembros que conforman la estructura. Sin embargo, estas características serán diferentes dependiendo de la zona de la estructura que estemos analizando. Es por ello que la persona a cargo de realizar el modelo, debe escoger cuidadosamente las propiedades lineales o no lineales que deben ser asignadas a los elementos según el comportamiento estructural que se desea evidenciar, conforme a los mecanismos de transferencia de carga que se generen y según las condiciones de borde del modelo.
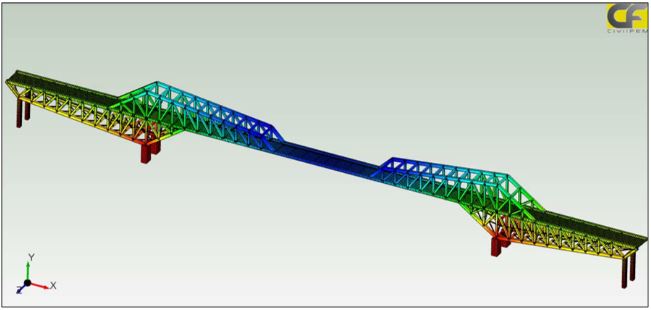
Figura 10: Modelo en FEM del Tokio Gate Brige. CivilFEM Software.
Procedimiento general para el modelado de puentes en elemento finito
En la mayoría de los casos se divide el proceso de modelado y análisis en elemento finito en los siguientes pasos:
- Idealización
Consiste en realizar una simplificación de la estructura real, mediante su representación con un modelo estructural, por ejemplo, un modelo de Shell en 3D. El modelo debe contemplar la geometría, condiciones de borde, cargas, etc. Por ejemplo, en el diseño de estructuras de concreto, es común asumir que el material es linealmente elástico. Generalmente las condiciones de borde en los soportes son simplificadas estableciéndolas como fijas o empotradas. En muchos casos pudiese ser importante definir la rigidez de los soportes según las características esfuerzo-deformación del material de apoyo (bearings).
- Discretización
En esta fase se divide el modelo estructural en elementos finitos, es decir, se realiza el mallado del modelo. Un mallado denso con elementos con poca distorsión, permiten respuestas más precisas. Sin embargo, se debe acotar que un mallado denso, a pesar de garantizar resultados precisos, requiere de una gran demanda computacional, como en el caso de los elementos Shell si lo comparamos con los elementos “Plate”.
- Análisis de elementos
En este paso se calculan las rigideces de los elementos. La rigidez interna del elemento en el análisis se aproxima con una función base. En los análisis mediante elemento finito se utiliza la integración numérica para lograr buenos resultados, sin embargo, esta integración se considera aproximada, incluso si se utiliza una cantidad suficiente de puntos de integración.
- Análisis estructural
Se calcula la matriz de rigidez del sistema mediante el ensamblaje de las matrices de rigidez de los elementos individuales con las respectivas condiciones de equilibrio y las condiciones geométricas. El sistema de ecuaciones puede ser resuelto para toda la estructura. Los ordenadores facilitan el poder considerar una gran cantidad de miembros en los procesos.
- Post proceso
En este paso se realizan los cálculos de esfuerzos en todos los elementos. Los esfuerzos se calculan en los puntos de integración; generalmente estos puntos no están situados en los nodos de los elementos. Los resultados presentados en los puntos de integración, son los resultados más exactos en un análisis en elemento finito. Frecuentemente los resultados presentados son de los nodos del elemento. Los resultados en los nodos son extrapolados a partir de los resultados en los puntos de integración.
- Manejo de resultados
Los resultados obtenidos de un análisis en elemento finito requieren de criterios sólidos y de una correcta interpretación por parte del proyectista. Los resultados estarán rodeados de incertidumbre, como consecuencia de las suposiciones en el comportamiento real de la estructura, y establecidas en el proceso de modelado. Cuando el análisis es de tipo Frame en 2D, los resultados pueden ser manejados con mucha mayor facilidad. Sin embargo, en análisis con elementos tipo Shell en 3D, se complica notablemente la interpretación de los resultados. Es por ello que sea común en este tipo de softwares, que los resultados se presenten de forma numérica combinados con escalas de colores que permitan una cómoda revisión y visualización de las solicitaciones, tal como se muestra a continuación.
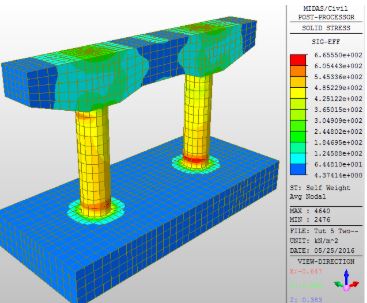
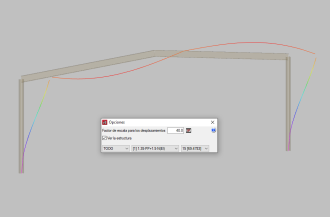
Figura 7.19: Visualización de Resultados de un Modelo de Pórtico de Apoyo de Puente en Elemento Finito (FEM).

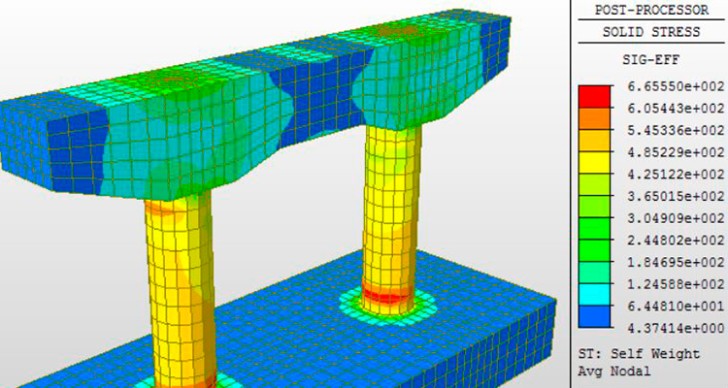
 Figura 1: Modelos tridimensionales de puentes.Fuente: MIDAS Information Technology Co.
Figura 1: Modelos tridimensionales de puentes.Fuente: MIDAS Information Technology Co.
 Figura 2: Modelos de puentes complejos.Fuente: MIDAS Information Technology Co.
Figura 2: Modelos de puentes complejos.Fuente: MIDAS Information Technology Co.


 Figura 4: Línea de influencia para diagrama de momento en modelo bidimensional.
Figura 4: Línea de influencia para diagrama de momento en modelo bidimensional.
 Figura 5: Superficie de influencia para diagrama de momento en modelo tridimensional.
Figura 5: Superficie de influencia para diagrama de momento en modelo tridimensional.
 Figura 6: Tablero cargado mediante un eje de carga.
Figura 6: Tablero cargado mediante un eje de carga.
 Figura 7: Flexión longitudinal del tablero.
Figura 7: Flexión longitudinal del tablero.
 Figura 8: Flexión transversal del tablero.
Figura 8: Flexión transversal del tablero.
 Figura 9: Deformación del tablero en un modelo tridimensional.
Figura 9: Deformación del tablero en un modelo tridimensional.
 Figura 10: Modelo en FEM del Tokio Gate Brige. CivilFEM Software.
Figura 10: Modelo en FEM del Tokio Gate Brige. CivilFEM Software.
 Figura 7.19: Visualización de Resultados de un Modelo de Pórtico de Apoyo de Puente en Elemento Finito (FEM).
Figura 7.19: Visualización de Resultados de un Modelo de Pórtico de Apoyo de Puente en Elemento Finito (FEM).