Autor
Jose Carlos Coya
Co-director del Máster Internacional en Cimentaciones y Estructuras de Contención y el Máster Internacional en Estructuras de Edificación con Cype en Zigurat Global Institute of Technology.
Categorias

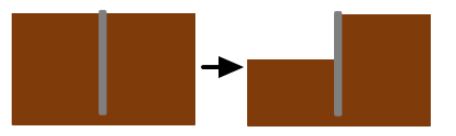
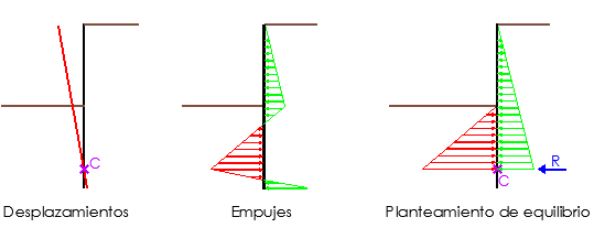 Figura 2.2 Modelo de cálculo de pantalla en voladizo
El modelo de cálculo se basa en suponer que la pantalla gira respecto a un punto C y por lo tanto el momento de todas las fuerzas que actúan en la pantalla es nulo respecto a ese punto. En el caso más simple, de terreno homogéneo sin sobrecargas, las fuerzas que actúan son el empuje activo en el trasdós, el empuje pasivo en el intradós y una reacción pasiva en la parte inferior del trasdós que se modela como R. En la parte enterrada el pasivo y el activo se neutralizan mutuamente.
El planteamiento del equilibrio de fuerzas y momentos permite determinar las incógnitas t0 (empotramiento de la pantalla) y R (contrarreacción).
Figura 2.2 Modelo de cálculo de pantalla en voladizo
El modelo de cálculo se basa en suponer que la pantalla gira respecto a un punto C y por lo tanto el momento de todas las fuerzas que actúan en la pantalla es nulo respecto a ese punto. En el caso más simple, de terreno homogéneo sin sobrecargas, las fuerzas que actúan son el empuje activo en el trasdós, el empuje pasivo en el intradós y una reacción pasiva en la parte inferior del trasdós que se modela como R. En la parte enterrada el pasivo y el activo se neutralizan mutuamente.
El planteamiento del equilibrio de fuerzas y momentos permite determinar las incógnitas t0 (empotramiento de la pantalla) y R (contrarreacción).
 Planteamiento del equilibrio
Analizando el equilibrio obtenemos
Planteamiento del equilibrio
Analizando el equilibrio obtenemos
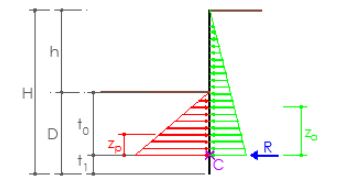
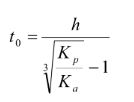 Blum propone añadir un 20 % a este valor para que puede desarrollarse la fuerza R suficiente para mantener el equilibrio. La longitud total de la pantalla es H=h+1,2·t0.
El diagrama de momentos supone un máximo en el trasdós de la zona empotrada.
Blum propone añadir un 20 % a este valor para que puede desarrollarse la fuerza R suficiente para mantener el equilibrio. La longitud total de la pantalla es H=h+1,2·t0.
El diagrama de momentos supone un máximo en el trasdós de la zona empotrada.
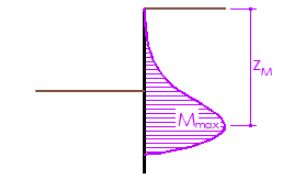 Diagrama de momentos
El valor del momento flector máximo (Mmax) es
Diagrama de momentos
El valor del momento flector máximo (Mmax) es
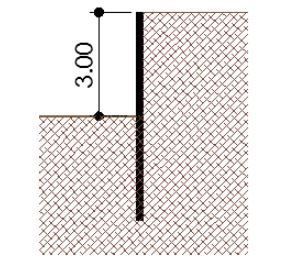
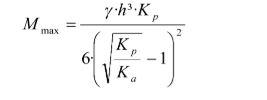 Ejemplo
Planteamos una pantalla con una excavación de 3 m un terreno granular con un ángulo de rozamiento interno ø’=30º y densidad g=18 kN/m³. Determinamos la profundidad de la clava y el momento flector máximo.
Ejemplo
Planteamos una pantalla con una excavación de 3 m un terreno granular con un ángulo de rozamiento interno ø’=30º y densidad g=18 kN/m³. Determinamos la profundidad de la clava y el momento flector máximo.
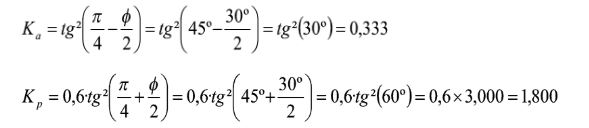 La profundidad del punto de giro es
La profundidad del punto de giro es
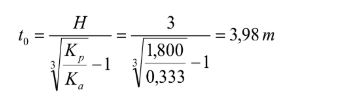 El incremento de la profundidad de clava t es
El incremento de la profundidad de clava t es
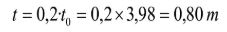 Por lo tanto la profundidad total de la clava es 3,98+0,80=4,78 m, que podríamos redondear a 4,80 m, lo que daría una pantalla total de 7,80 m.
El valor del momento flector máximo (Mmax) es:
Por lo tanto la profundidad total de la clava es 3,98+0,80=4,78 m, que podríamos redondear a 4,80 m, lo que daría una pantalla total de 7,80 m.
El valor del momento flector máximo (Mmax) es:
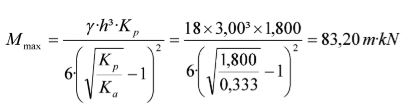
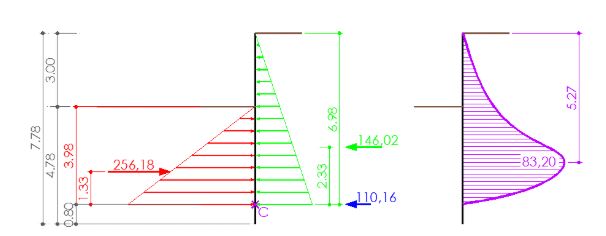 Podemos resumir el proceso en una hoja de cálculo.
Podemos resumir el proceso en una hoja de cálculo.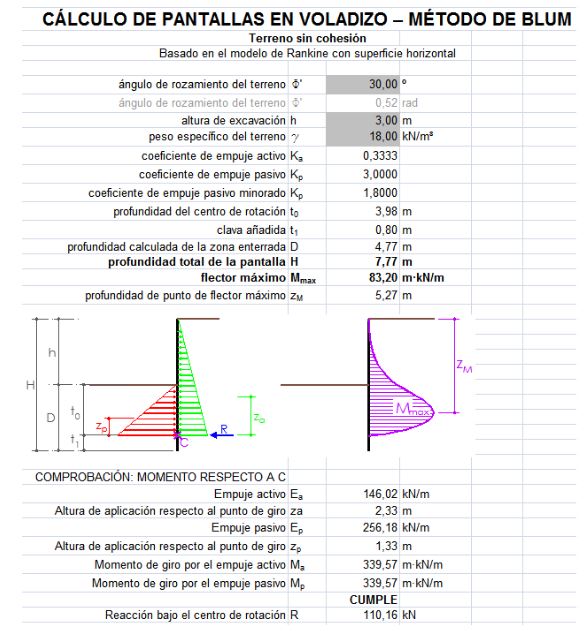
 Modelo basado en muelles y ley de empuje del terreno/deformación
Este método de análisis permite estudiar pantallas con varios puntos de sujeción y considerar en el cálculo el proceso de ejecución, fundamental en el caso de pantallas. Asimismo, permite estimar el movimiento horizontal de la pantalla.
Los muelles que simulan el terreno tienen propiedades distintas en función del tipo de desplazamiento que tengan, sea alargamiento o acortamiento.
Si calculamos con Cype Muros pantalla un muro pantalla en voladizo, vemos que el comportamiento es muy similar al previsto por Blum, aunque el momento flector sale menor.
Modelo basado en muelles y ley de empuje del terreno/deformación
Este método de análisis permite estudiar pantallas con varios puntos de sujeción y considerar en el cálculo el proceso de ejecución, fundamental en el caso de pantallas. Asimismo, permite estimar el movimiento horizontal de la pantalla.
Los muelles que simulan el terreno tienen propiedades distintas en función del tipo de desplazamiento que tengan, sea alargamiento o acortamiento.
Si calculamos con Cype Muros pantalla un muro pantalla en voladizo, vemos que el comportamiento es muy similar al previsto por Blum, aunque el momento flector sale menor.
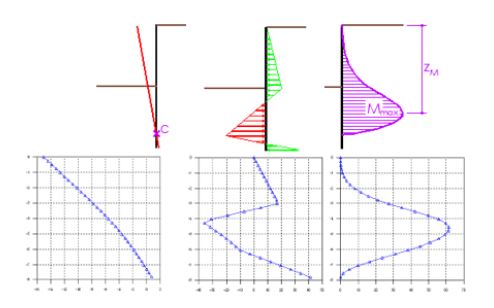 Comparativa de desplazamientos, empujes y flectores por Blum y Winkler
Ahora bien, el método de Winkler nos permite considerar más parámetros. Por ejemplo, veamos qué ocurre con diferentes tipos de terreno.
Comparativa de desplazamientos, empujes y flectores por Blum y Winkler
Ahora bien, el método de Winkler nos permite considerar más parámetros. Por ejemplo, veamos qué ocurre con diferentes tipos de terreno.
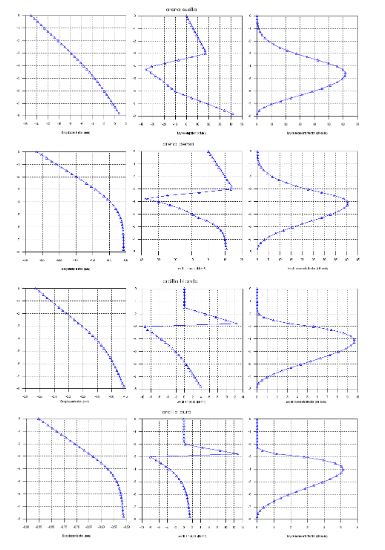 Comparativa de desplazamientos, empujes y flectores con distintos terrenos
Con Cype Muros pantalla podemos, además, definir diferentes estratos, definir el nivel freático, introducir cargas en superficie, analizar la estabilidad global y, finalmente, obtener el armado.
Comparativa de desplazamientos, empujes y flectores con distintos terrenos
Con Cype Muros pantalla podemos, además, definir diferentes estratos, definir el nivel freático, introducir cargas en superficie, analizar la estabilidad global y, finalmente, obtener el armado.
Jose Carlos Coya