Autor
Carles Romea
Co-director del Máster Internacional en Estructuras de Edificación con CYPE y Director del Máster de Estructuras Metálicas y Mixtas en Edificación en en Zigurat Global Institute of Technology.
Algunos comentarios sobre el pandeo
Categorias
En el ya lejano 1759, se publicó, en francés, el trabajo del matemático Leonhard Euler, “Sur la force des colonnes” (Acerca de la fuerza sobre columnas), trabajo que está recogido en las “Mémoires de l’académie Royales des Sciences et le Belle-lettres” de 1757 en Berlin. Este trabajo, por sus importantes consecuencias ulteriores sobre el diseño y cálculo de estructuras merece algunos comentarios.
El primero es darnos cuentas que en pleno siglo XVIII, las academias aun no distinguían entre ciencias y letras, y que en una misma institución se recogían todas aquellas disciplinas que tenían que ver con el conocimiento. Estaba gestándose y aún por venir la revolución industrial.
Siendo F la fuerza máxima que puede soportar una columna sin “plegarse” ( en palabras de Euler). Y añade que para entender bien esta expresión, hemos de fijarnos en la expresión Ekk que bautiza como “Moment du reffort”, ya que π, es una expresión trigonométrica conocida, y a es la altura de la columna, y son por tanto valores conocidos que se refieren a conceptos claros. No así su “momento du reffort”. Y aquí Euler nos explica que esta expresión es una manera de medir su “raideur”, su rigidez. Modernamente sabemos que la rigidez de una barra se mide a partir de su longitud, de su módulo de deformación E, y de su inercia o área. Euler ya lo intuye en su fórmula original
Euler parte de la idea, cierta, que la altura de la columna y el espesor de la pared de la sección de la columna, sección resistente diríamos hoy, juegan un papel esencial en su comportamiento bajo una acción de compresión. A tal efecto llevó a cabo diversos experimentos para comprobarlo. Y además llegó a la conclusión de que conociendo la “rigidez” de la columna se podía deducir el radio de curvatura que originaría la aplicación de una fuerza, dado que ambos efectos deberían ser proporcionales.
Según Euler, de su fórmula se deduce que “contra mayor altura tiene una columna, menor es su capacidad para soportar una carga”, pero además nos afirma que “dicha fuerza es inversamente proporcional al cuadrado se su altura”. “Si tenemos dos columnas, una de doble altura que la otra, con los mismos materiales y sección, podemos afirmar que la más alta solo podrá soportar un cuarto de la carga que la primera”.
Nos habla de la fuerza crítica o fuerza máxima que podrá soportar la columna, a partir de la cual, podremos tener una deformación elástica de pandeo (fuerza de “plegado”). Como diferencia notable vemos que la rigidez (raideur) que en la versión inicial venia expresada por el termino Ekk, toma ahora la expresión EI, y es una medida de la rigidez. Durante el siglo XIX, se define el concepto de inercia, directamente relacionado con la superficie resistente de la sección de la columna. Recordemos que se calcula a partir del doble momento estático del área, de ahí que el termino k k=k2, no deja de ser pues la medida de la inercia, aunque Euler lo deduce a partir de un modelo puramente matemático. Y Euler introduce también el concepto de la influencia del material, y nos habla en su escrito de la piedra o la madera (la fundición o el acero aun no existían). El valor de E, constante, hoy lo asociamos con el módulo de Young, que efectivamente, nos informa sobre la rigidez del material de construcción de la columna. Euler ya lo intuyó de forma magistral en sus hipótesis de cálculo.
De acuerdo pues con la mecánica desarrollada durante el siglo XIX, la relación entre la inercia y el área de una sección, nos define el radio de inercia al cuadrado. Por tanto el radio de inercia vendrá expresado por:
Y es una medida mecánica de cuan separada se encuentra la masa resistente respecto de un eje de referencia. A mayor radio de inercia mayor inercia, para una misma área, cantidad de superficie resistente de una sección.
Y ahí nace un nuevo concepto, mucho más claro, como es el concepto de esbeltez que, se define como la relación entre la altura L, y el radio de inercia. Generalmente pudiera parecer que la altura, como valor absoluto, es la responsable del pandeo. Y no es así, ya que además, esta altura ha de estar en relación con su sección. Veamos un ejemplo clásico.
Portada de la edición original del trabajo de L.Euler
Euler publica este trabajo como consecuencia, en un suplemento dice él, de su investigación principal sobre superficies laminares elásticas, y afirma que “he encontrado una regla para evaluar la resistencia de una columna que, me pareció de entrada, muy apreciable. Se trata de determinar el peso que puede soportar una columna, sin plegarse”. Evidentemente la palabra pandeo, todavía no ha sido acuñada, pero sí que, Euler, nos da la clave de su hallazgo. Y lo resume en una expresión matemática siguiente: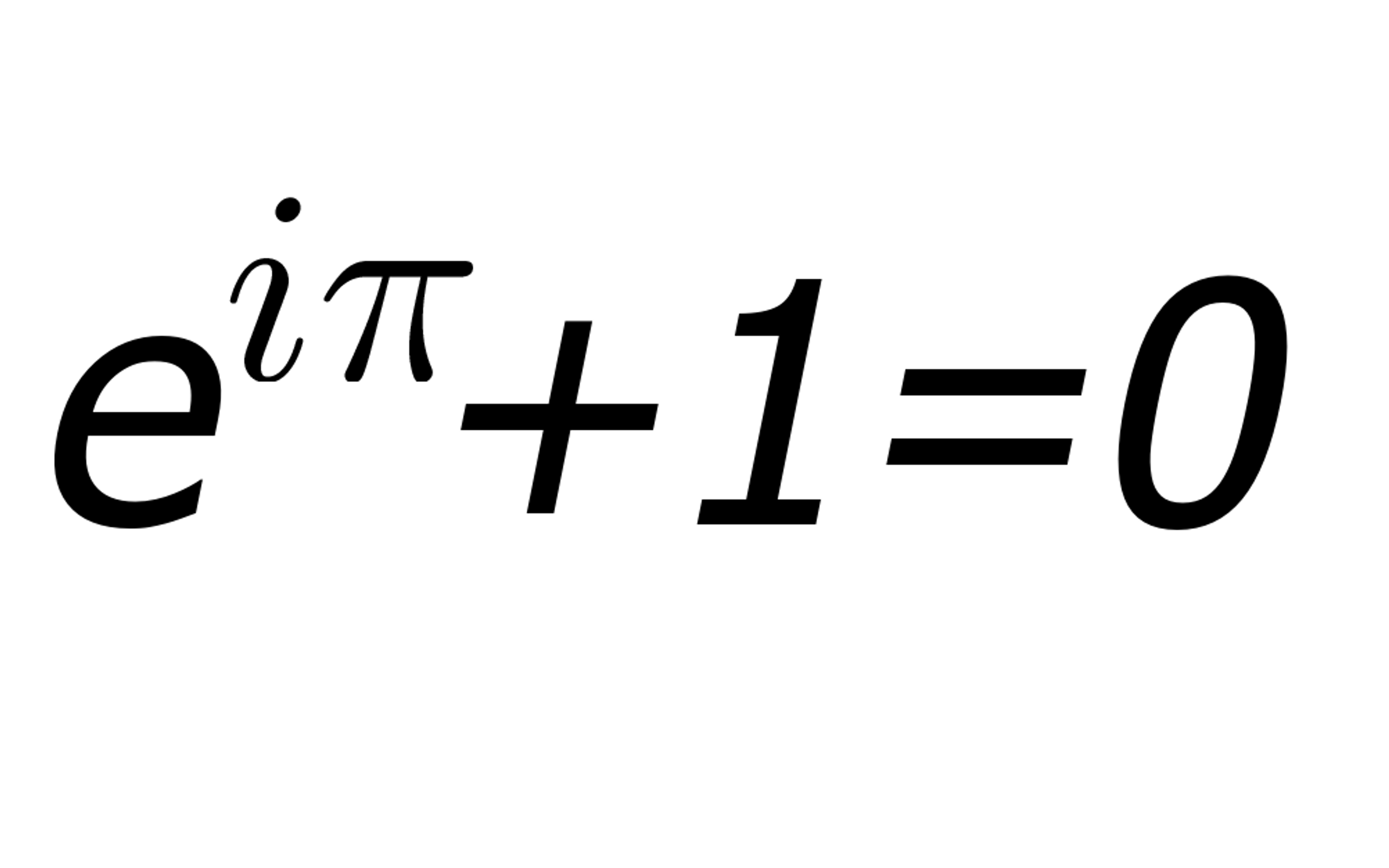Siendo F la fuerza máxima que puede soportar una columna sin “plegarse” ( en palabras de Euler). Y añade que para entender bien esta expresión, hemos de fijarnos en la expresión Ekk que bautiza como “Moment du reffort”, ya que π, es una expresión trigonométrica conocida, y a es la altura de la columna, y son por tanto valores conocidos que se refieren a conceptos claros. No así su “momento du reffort”. Y aquí Euler nos explica que esta expresión es una manera de medir su “raideur”, su rigidez. Modernamente sabemos que la rigidez de una barra se mide a partir de su longitud, de su módulo de deformación E, y de su inercia o área. Euler ya lo intuye en su fórmula original
Euler parte de la idea, cierta, que la altura de la columna y el espesor de la pared de la sección de la columna, sección resistente diríamos hoy, juegan un papel esencial en su comportamiento bajo una acción de compresión. A tal efecto llevó a cabo diversos experimentos para comprobarlo. Y además llegó a la conclusión de que conociendo la “rigidez” de la columna se podía deducir el radio de curvatura que originaría la aplicación de una fuerza, dado que ambos efectos deberían ser proporcionales.
Según Euler, de su fórmula se deduce que “contra mayor altura tiene una columna, menor es su capacidad para soportar una carga”, pero además nos afirma que “dicha fuerza es inversamente proporcional al cuadrado se su altura”. “Si tenemos dos columnas, una de doble altura que la otra, con los mismos materiales y sección, podemos afirmar que la más alta solo podrá soportar un cuarto de la carga que la primera”.
Condiciones de contorno
Actualmente, si consultamos los libros de estructuras modernos, nos aparecen las siguientes expresiones, muy parecidas a las expuestas, en su versión original por el propio Euler:
Nos habla de la fuerza crítica o fuerza máxima que podrá soportar la columna, a partir de la cual, podremos tener una deformación elástica de pandeo (fuerza de “plegado”). Como diferencia notable vemos que la rigidez (raideur) que en la versión inicial venia expresada por el termino Ekk, toma ahora la expresión EI, y es una medida de la rigidez. Durante el siglo XIX, se define el concepto de inercia, directamente relacionado con la superficie resistente de la sección de la columna. Recordemos que se calcula a partir del doble momento estático del área, de ahí que el termino k k=k2, no deja de ser pues la medida de la inercia, aunque Euler lo deduce a partir de un modelo puramente matemático. Y Euler introduce también el concepto de la influencia del material, y nos habla en su escrito de la piedra o la madera (la fundición o el acero aun no existían). El valor de E, constante, hoy lo asociamos con el módulo de Young, que efectivamente, nos informa sobre la rigidez del material de construcción de la columna. Euler ya lo intuyó de forma magistral en sus hipótesis de cálculo.
De acuerdo pues con la mecánica desarrollada durante el siglo XIX, la relación entre la inercia y el área de una sección, nos define el radio de inercia al cuadrado. Por tanto el radio de inercia vendrá expresado por:
Y es una medida mecánica de cuan separada se encuentra la masa resistente respecto de un eje de referencia. A mayor radio de inercia mayor inercia, para una misma área, cantidad de superficie resistente de una sección.
Y ahí nace un nuevo concepto, mucho más claro, como es el concepto de esbeltez que, se define como la relación entre la altura L, y el radio de inercia. Generalmente pudiera parecer que la altura, como valor absoluto, es la responsable del pandeo. Y no es así, ya que además, esta altura ha de estar en relación con su sección. Veamos un ejemplo clásico.
Dos edificios con alturas similares pero de esbelteces muy diferentes
Por eso, a partir de la formulación anterior, y siguiendo el espíritu inicial de Euler, podamos hablar de Área A = k k, e introducir el concepto de esbeltez, con un significado mecánico muy claro, en lugar del concepto de altura de la columna. ¿Por qué? Sabemos que las ecuaciones diferenciales lineales tienen siempre una solución general, y luego soluciones particulares en función de las Condiciones de contorno, como muy bien documentó Euler en su trabajo. Pues bien en las barras comprimidas, las condiciones de contorno se refieren al vínculo de sus nudos extremos. Sabemos que dichos nudos extremos, pueden ser libres, articulados o empotrados, de una manera ideal. En la realidad, su estado será intermedio entre los modelos teóricos propuestos como solución matemática al problema. Pues bien, estas condiciones de contorno, condicionan la deformabilidad de la barra, dado que en el caso de los empotramientos, los extremos, por definición tienen el giro impedido, lo cual lleva a replantear los puntos de la barra que si pueden girar, y que generalmente corresponden a puntos de inflexión de la curva elástica de Euler. De ahí que, cuando hablamos de longitud de la barra, debamos corregir el concepto de longitud y añadirle “de pandeo”, es decir entre puntos de inflexión. De acuerdo con la notación clásica, veremos que podemos contemplar pues barras comprimidas, con los dos extremos completamente empotrados, ambos articulados, empotrado articulado o bien empotrado libre. Cada caso corresponde a una condición de contorno diferente y por tanto una solución diferente de la ecuación diferencial general: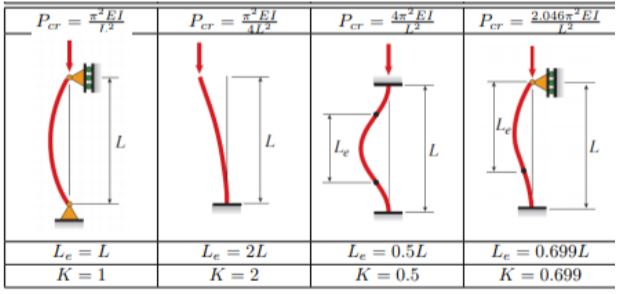
Puntos de inflexión que marcan la longitud de pandeo
Pues bien, finalmente, tenemos que el concepto de esbeltez será la relación entre la longitud de pandeo Lp, diferente de la longitud geométrica, según las condiciones de contorno, i el radio mínimo de giro de la sección. Es decir que, para controlar el pandeo tendremos siempre tres estrategias. • Aumentar la inercia de la sección, es decir el área resistente • Actuar sobre las condiciones de contorno, reduciendo la longitud de pandeo • Finalmente, mejorar la rigidez del material
